- Острый угол от $0^{\circ }$ до $90^{\circ }$. Его синус = отношение "катет : гипотенузу" в прямоугольном треугольнике.
- А как понимать синус и косинус тупого угла от $90^{\circ }$ до $180^{\circ }$? Прямоугольного $\bigtriangleup$ нет!
- Углы $200^{\circ }$, $300^{\circ }$ можно увидеть на окружности в виде секторов. Но что есть их синус?
- А как быть с большими углами $1340^{\circ }$ ? Они нужны при нескольких оборотах: двигатель, вращение фигуриста.
- Что есть отрицательный угол? Как это "увидеть", изобразить? Для всего этого нужна Е.Т.О.
Единичная тригонометрическая окружность - Е.Т.О.
Е.Т.О. используется для удобного изображения углов в виде точек на окружности.
Радиус равен единице. $OA=OB=OC=OD=1$ . Е.Т.О. снабжена координатными осями: ось $x$, ось $y$.
Каждому углу соответствует своя точка на Е.Т.О. , получающаяся в итоге поворота радиуса на этот угол!
- Начало отсчета углов из правой точки $A=(1;0)$. Эта точка соответствует $0^{\circ }$ градусам.
- Для отмерения угла радиус-вектор $OA$ проворачивается из начального положения $A=(1;0)$
- для положительных углов вверх, против часовой стрелки, провернув на требуемый угол
- Для отрицательных углов надо крутить из $A$ вниз, по часовой стрелке до нужного угла.
- При больших углах потребуется совершить несколько оборотов, отсюда периодичность.
- "$+$" - против часовой стрелки. "$-$" - по часовой стрелке.

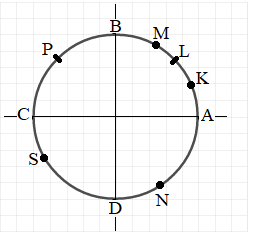

Какому углу какая точка соответствует на Е.Т.О ?
- $60^{\circ }$ соответствует точка $M$ . Из точки $A$ вверх так, чтоб угол $MOA$ стал $60^{\circ }$ .
- $135^{\circ }$ попадает в $P$ . Радиус провернем от $OA$ вверх, против часовой стрелки до $OP$, чтоб угол $POA=135^{\circ }$ .
- $-90^{\circ }$ градусов попадает на $D$ . Поворот из $A$ по часовой стрелке. $DOA=90^{\circ }$ .
- $210^{\circ }$: от $OA$ вверх, против часовой стрелки, мимо $K$, $M$, $P$, $B$, $L$, $C$ и доберемся до $S$, $SOA=210^{\circ }$ .
- Проследим за нужными поворотами , "прокрутками" и убедимся в соответствии углов и точек:
- $0^{\circ }=A$ $30^{\circ }=K$ $45^{\circ }=L$ $60^{\circ }=M$ $90^{\circ }=B$ $135^{\circ }=P$ $180^{\circ }=C$ $-150^{\circ }=S$ $270^{\circ }=D$
- $300^{\circ }=N$ $-60^{\circ }=N$ $-90^{\circ }=D$ $-150^{\circ }=S$ $-180^{\circ }=C$ $-225^{\circ }=P$ $-270^{\circ }=B$ $-330^{\circ }=K$ $-360^{\circ }=A$
- Периодичность: некоторые углы "попадают" в одни и те же точки. Их различие - полные обороты, кратность $360^{\circ }$
- Каждый угол представлен одной точкой! Каждая точка изображает бесконечное количество углов ... $\pm 360^{\circ } \cdot n$ !
Угол $\to$ Точка на Е.Т.О. $\to$ координаты точки
Е.Т.О имеет четыре четверти - те же координатные четверти системы координат: во 2-ой четверти х - координата отрицательная!
Координаты соответствующей углу $\alpha$ точки на Е.Т.О. находятся по "своим" прямоугольным треугольникам с гипотенузой $=1$ и углом "от $\alpha$".
Прямоугольные треугольники для точки угла состоят из катетов - проекций на осях и гипотенузы = 1, радиус Е.Т.О.
Нахождение координат точки "хорошего угла":
Углы, кратные $90^{\circ }$ попадают в пересечения Е.Т.О с осями - в "вершины" с координатами ($0,\pm1$) или ($\pm1,0$), значит координаты точек таких углов принимают значения либо $0$, либо $1$, либо $-1$.
Углы, кратные четному числу раз по $90$ градусов попадают на горизонтальную ось $x$ в точки с координатами $\left(\pm1;0\right)$ . Например, это углы: $180$, $0$, $-540$, $-180$ .
Углы, кратные нечетному числу раз по $90^{\circ }$ градусов попадают на вертикальную ось $y$ в точки с координатами $\left(0;\pm1\right)$ . Например, это углы: $-90$, $270$, $-270$, $90$ .
Углы, кратные $45^{\circ }$ градусам попадают в середины дуг четвертей или в вершины. (левый рисунок).
Углы, кратные $30^{\circ }$ делят дуги четвертей на три равные части или попадают в вершины. (средний рис.)
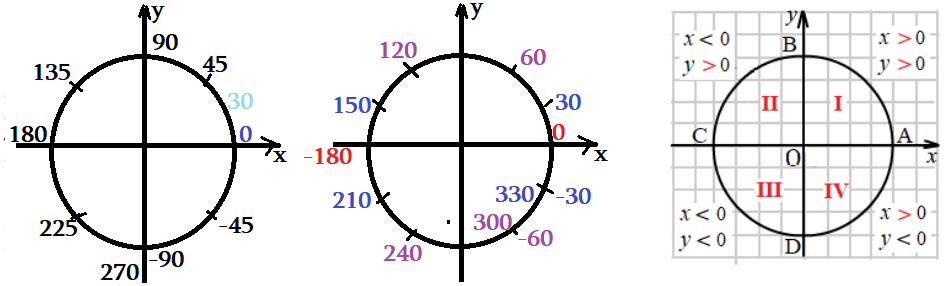
"Приводимые" к $45^{\circ }$ : - это все углы, кратные $45^{\circ }$ градусам.
- абсцисса и ордината образуют равнобедренный прямоугольный треугольник с гипотенузой $= 1$ и двумя углами по $45$ .
- из т. Пифагора $OP^2+PT^2=OT^2$ получаем $x^2+x^2=1$ $\Rightarrow $ оба катета $x=\frac{\sqrt{2}}{2}$ .
- во всех точках - серединах четвертей координаты будут такими же: $\left(\pm\frac{\sqrt{2}}{2};\pm\frac{\sqrt{2}}{2}\right)$.
"Приводимые к $30^{\circ }$, $60^{\circ }$ ": прямоугольные $\bigtriangleup$ типа $OPM$ с гипотенузой $1$ и острый угол $30^{\circ }$ .
- Один угол $30^{\circ }$ значит катет = половине гипотенузы $MP=\frac{OP}{2}=\frac{1}{2}$ , катет $OP=\sqrt{OM^2-MP^2}=\sqrt{1-\frac{1}{4}}=\frac{\sqrt{3}}{2}$ .
- Тогда для всех несократимых $\frac{n\cdot\pi}{6}$ или $\frac{m\cdot\pi}{3}$ координатами будут $\pm\frac{1}{2}$ или $\pm\frac{\sqrt{3}}{2}$ .
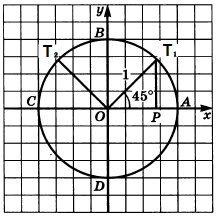
Пример 1: Найти координаты точки $T_{315^{\circ }}$ , соответствующие углу $315^{\circ }$ .
- Прокрутим $315^{\circ }$ ... Точка попадает в середину $4$-ой четверти ... $x>0$ $y<0$
- Опустим проекции: образуется равнобедренный прямоугольный треугольник ... оба катета равны $\frac{\sqrt{2}}{2}$
- Значит, координаты точки $T_{315^{\circ }} = \left(\frac{\sqrt{2}}{2};-\frac{\sqrt{2}}{2}\right)$
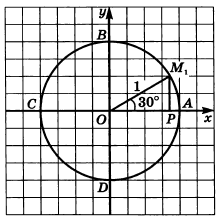

Пример 2: Найти координаты точки $T_{-240^{\circ }}$ , соответствующие углу $-240^{\circ }$ .
- Против часовой: $-240^{\circ }$ попадает в верхнюю треть $2$ -ой четверти. Кстати, там $120^{\circ }$ .
- Мысленно начертим треугольник из радиуса, абсциссы и ординаты. $x<0$ $y>0$
- Треугольник получится такой же, как $OPM$ . С углом $30^{\circ }$ ... только перевернутый.
- Катеты те же, меньший катет $\frac{1}{2}$ - абсцисса, больший $\frac{\sqrt{3}}{2}$ - ордината.
- Значит $x=-\frac{1}{2}$ , $y=\frac{\sqrt{3}}{2}$ ( $2$-ая четверть). $T_{-240^{\circ }}=(-\frac{1}{2};\frac{\sqrt{3}}{2})$
Пример 3: Найдите $T_{210^{\circ }}$ .
- Угол $T_{210^{\circ }}$ попадает в 3-ю четверть. $x$ - абсцисса "длиннее" $y$ - ординаты. $x<0$ $y<0$
- Значит, $y=-\frac{1}{2}$ $x=-\frac{\sqrt{3}}{2}$ . $T_{210^{\circ }}=(-\frac{\sqrt{3}}{2};-\frac{1}{2})$
Пример 4: Указать приближенные координаты точки $T_{128^{\circ }}$
- Смотрим Е.Т.О. "в клетках". Радиус = $1$ = $10$ клеток. Каждая клетка = $0,1$
- "На глаз" ищем точку угла $128^{\circ }$ : она находится во второй четверти, ближе к верхней трети. $x<0$ $y>0$
- Смотрим координаты этой точки: опускаем перпендикуляры на оси координат ... "на глаз", сколько клеток?
- Видно, что $x$ абсцисса около $6$ клеток. Но во второй четверти она отрицательна, значит $x\approx -0,6$.
- $y$ - ордината "отмеряет" $8$ клеток, $y\approx0,8$ . Значит, $T_{128^{\circ }} \approx (-0,6;0,8)$
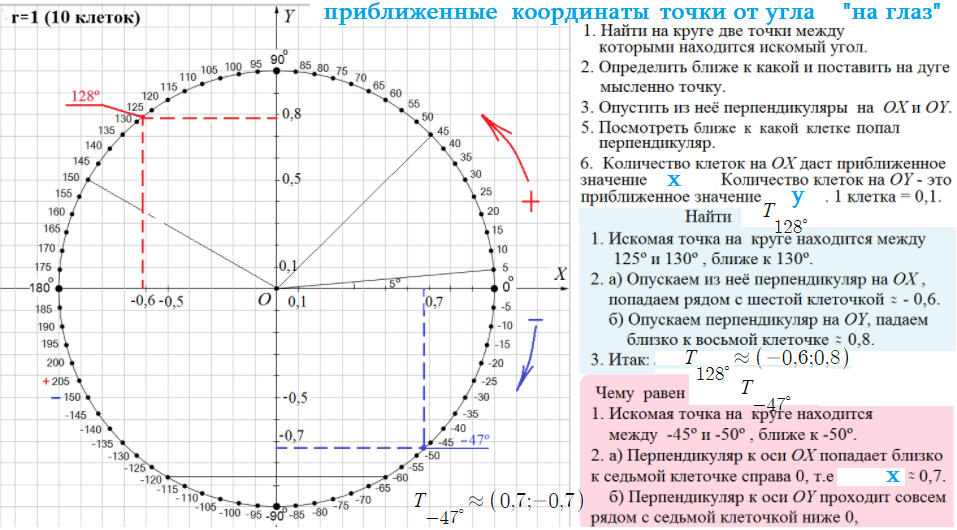
Пример 5: Найти приближенные координаты $T_{-47^{\circ }}$
- Отрицательный угол $-47^{\circ }$ проворачиваем по часовой стрелке. "Упадет" в середину 4 - ой четверти. $x>0$ $y<0$
- "На глаз" видно, что координаты примерно по $7$ клеток. Учтем знаки: $T_{-47^{\circ }} \approx (0,7;-0,7)$
$T_{10^{\circ }}=(0,98480775;0,17364817)$ $T_{20^{\circ }}=(0,9396926;0,3420201)$ $T_{15^{\circ }}=(0,9659258;0,25881904)$
Упражнения A: Визуализация: Поворот углов, нахождение соответствующих точек, координаты. Вычисление точных или приближенных значений координат точек на Е.Т.О.
Упражнения B: Координаты точек на Е.Т.О для углов, заданных в градусах. Свойства.
Послесловие:
1. Надо научиться легко проворачивать угол на Е.Т.О. Если потребуется делать обороты, докручивать до нужной точки.
2. Уметь находить для угла соответствующую точку на Е.Т.О; определять в какую четверть попадает угол, в верхнюю или нижнюю часть Е.Т.О.
3. Для всех "хороших" углов быстро находить координаты точки на Е.Т.О. ... Видеть нужные треугольники, проекции!
3. Для углов быстро находить примерную точку "попадания", "на глаз" определять приближенное значение координат соответствующей точки на Е.Т.О.
