Скрещивающиеся прямые - не параллельны, не имеют общих точек, не пересекаются.
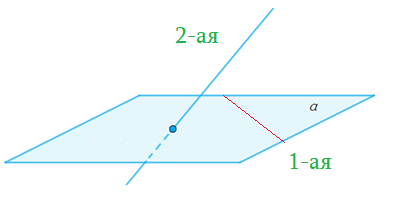
Признаки и характеристики скрещивающихся прямых
- 1-ая прямая лежит в плоскости, а 2-ая пересекает плоскость в точке не из 1-ой, то прямые скрещивающиеся.
- Через каждую из скрещивающихся прямых проходит плоскость, параллельная другой прямой. Единственная.
- Скрещивающиеся $a$ и $b$ : есть пара пареллельных плоскостей $\alpha$ и $\beta$, таких что $a\in \alpha$, $b\in \beta$
Углы и Расстояния между скрещивающимися прямыми
- У любой пары скрещивающихся прямых $AB$ и $MK$ есть единственная пара параллельных плоскостей $(a)$ и $(b)$ , содеражащих эти прямые.
- Угол м\ж скрещивающимися $\angle (AB;MK)$ равен углу между любым параллельным $M_1K_1\parallel MK$ прямым из (a) и прямым $AB$
- $\angle (AB;MK)$ $=$ $\angle (AB;M_1K_1)$ $=$ $\angle K_1OB$
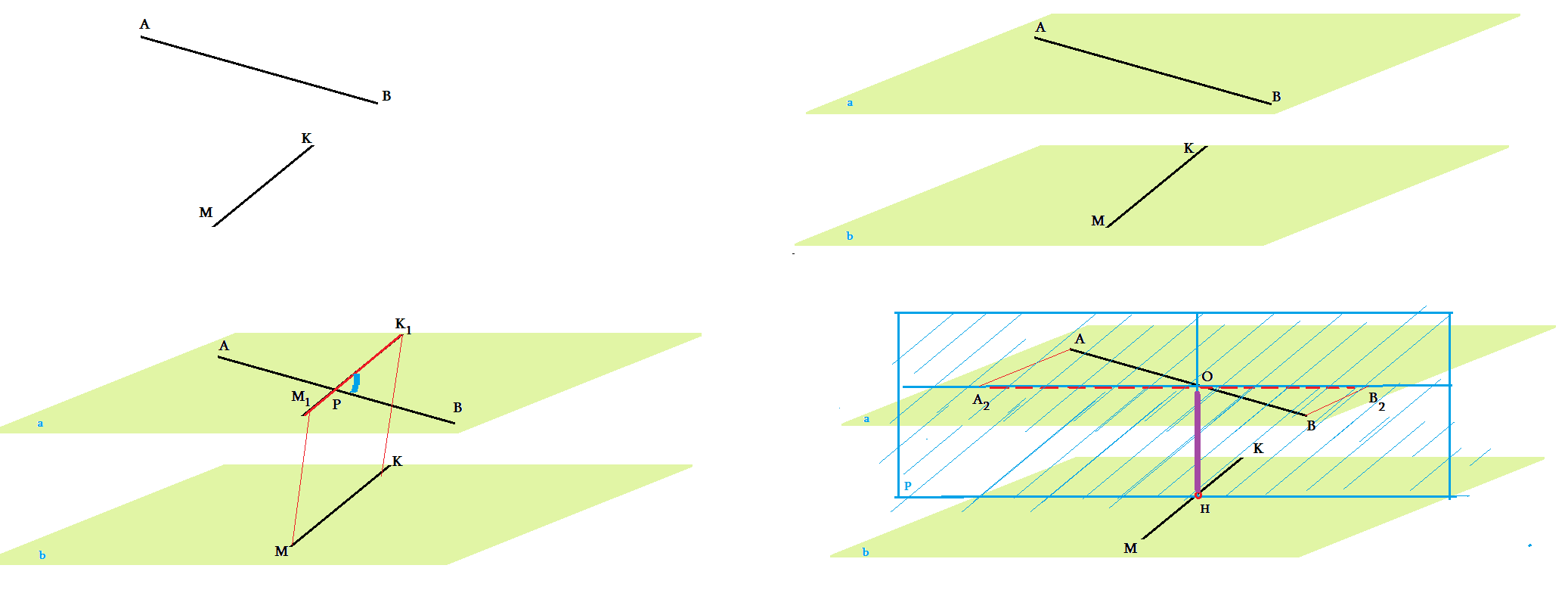
- Расстояние м\ж скрещивающимися $\bigtriangleup (AB;MK)$ - кратчайший путь от одной прямой до другой. минимальный отрезок.
- равен $\bigtriangleup (AB;MK)=\bigtriangleup (a;b)$ расстоянию между параллельными плоскостями $(a)\parallel (b)$, $AB\in (a)$, $MK\in (b)$
- Если построить перпендикулярную $(p)$ плоскость к одной из них: $(p)\perp MK$, $OH\perp MK$, $OH\in (p)$ ....
- Спроецировать на эту плоскость обе прямые: проекция $MK$ - точка $H$ , проекция $AB$ - прямая $A_2B_2$ , тогда ...
- $\bigtriangleup (AB;MK)=\bigtriangleup (H;A_2B_2)=HO$, расстоянию между проекциями скрещивающихся на перпендикулярную плоскость
- Кратчайший путь $HO\perp MK$, $HO\perp AB$. Обычно находится как высота $\bigtriangleup HA_2B_2$
Задача 1: В прямоугольном параллелепипеде $ABCDMNKL$ найти угол между скрещивающимися прямыми $AN$ и $BK$, если известны ребра $BA=36$, $BN=15$, $BC=20$
- Как находить угол между двумя стереометрическими объектами? по алгоритму параллельных переносов, совмещений.
- Свойство инвариантности углов при параллельном переносе стереометрических объектов - прямых, плоскостей:
- Если объекты $A$ и $B$ параллельны соответственно $A'$ и $B'$, то углы между парами равные: $\angle \left(A;B\right)=\angle \left(A';B'\right)$
- В нашем случае, $BK\parallel AL$, поэтому равны углы $\angle \left(AN;BK\right)=\angle \left(AN;AL\right)=\angle NAL$
- Перетащим $BK$ по плоскости $BKLA$ вдоль $BA$ до совмещения с точкой $A$. Тогда $BK$ совметится с отрезком $AL$.
- Итак, мы ищем угол $\angle NAL$. Найдем его через теорему косинусов в треугольнике $ANL$ для угла $\angle NAL$ :
- *** $NL^2=AN^2+AL^2-2\cdot AN\cdot NL\cdot \cos \angle NAL$
- Стороны $AN$, $NL$ и $AL$ можем признать диагоналями граней - прямоугольников, значит, найти их по теоремам Пифагора.
- Решение: $AN=\sqrt{36^2+15^2}=39$ $AL=\sqrt{20^2+15^2}=25$ $NL=\sqrt{36^2+20^2}=4\cdot \sqrt{106}$
- Из теоремы косинусов $\cos \angle NAL=\frac{AN^2+AL^2-NL^2}{2\cdot AN\cdot AL}=\frac{39^2+25^2-16\cdot 106}{2\cdot 39\cdot 25}=\frac{450}{1950}=\frac{3}{13}$ Ответ: $\angle NAL=\arccos \frac{3}{13}$
- Признак: $NAL$ - плоскость угла: $AN\in NAL$ и $BK\parallel NAL$
case I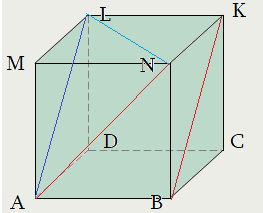 
case II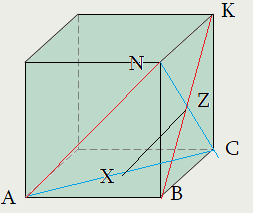 
Алгоритм: нахождение угла между прямыми путем параллельного переноса (демонстрация по II, прямые $AN$, $BK$ ):
- 1-ый шаг: Выбираем точку, в которой хотим совместить прямые. Например, точку $Z$ - середину отрезка $BK$.
- 2-ой шаг: Для прямой $AN$ определим плоскость "скольжения" - плоскость, содержащая эту прямую и точку $Z$. Это $ANC$
- 3-ий шаг: Двинем прямую $AN$ по плоскости $ANC$ оставаясь параллельно "как стержень". Она совместится с отрезком $ZX$.
- 4-ый шаг: Что за точка $X$ ? угол $\angle XZB$ - именно то, что нам нужно: $\angle XZB=\angle \left(XZ;BK\right)=\angle \left(AN;BK\right)$.
Признак: - увидеть ту главную плоскость угла , которая параллельна обеим скрещивающимся прямым. Здесь это $XZB$.
Сохранение угла при параллельных переносах, сдвигах прямой или плоскости, составляющих этот угол:
- м/ж прямой и прямой $\angle (AB;MN)=\angle (A_1B_1;M_1N_1)$ если $AB\parallel A_1B_1$ $MN\parallel M_1N_1$
- Если сдвинуть параллельно самому себе прямую или плоскость, то угол с другим объектом не изменится!
Задача 2: В правильной треугольной призме все ребра 1. Найти косинус угла $\angle \left(AB;CM\right)$
- $ABCMNK$ правильная призма: в основании правильный $\bigtriangleup ABC$ , ребро $BN$ перпендикулярно основанию.
- Нужен угол между $AB$ и $CM$. Выберем Точкой совмещения $M$. Прямая $CM$ уже проходит через нее.
- Прямая $AB$ и точка $M$ лежат в плоскости $ABNM$. Значит, $ABNM$ - плоскость сколжения. $AB$ перейдет в $MN$.
- Путем параллельного совмещения $AB$ с $MN$ мы устоновили, что искомый угол - это $\angle CMN$.
- Косинус угла $\angle CMN$ можно найти по теореме косинусов треугольника $CMN$: $\cos \angle CMN=\frac{CM^2+MN^2-CN^2}{2\cdot CM\cdot MN}$
- Признак: $CMN$ - плоскость угла: $AB\parallel CMN$ и $MC\in CMN$
k задачe 2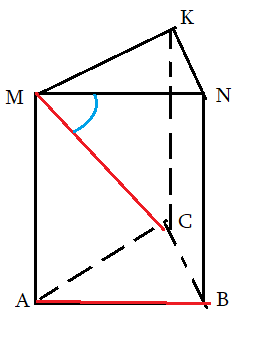 
к задаче 3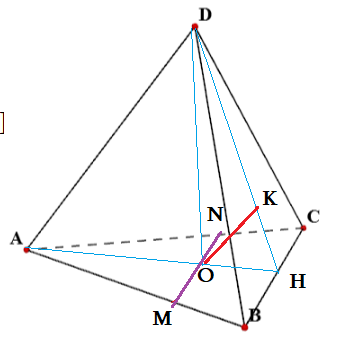 
Задача 3: В правильном тетраэдре $DABC$ все ребра 1 см. Найти угол между $AD$ и $BC$.
- Для нахождения угла, совместим "движениями" наши прямые в точку $O$ - основание высоты $DO$ .
- В правильном тетраэдре в основании равносторонный треугольник $DABC$, высота пирамиды попадает в центр окружностей.
- Точка $O$ - пересечение высот, медиан, биссектрис. $O$ лежит на высоте $AH$ , $DH$ - высота грани $BDC$.
- В точке $O$ проведем прямую параллельную прямой $BC$. Им будет линия $MN$
- В точке $O$ проведем прямую $OK$, параллельную $AD$. Она будет лежат в плоскости $ADH$ Значит, $K\in DH$.
- Итак, "взамен" наших $AD$ и $BC$ мы получили прямые $OK$ и $MN$ : $OK\parallel AD$, $MN\parallel BC$
- по свойству углов при параллельном переносе $\angle \left(AD;BC\right)=\angle \left(OK;MN\right)=\angle MOK$
- Найти $\angle MOK$ ? Легко! учтите, что у нас правильный тетраэдр и находите.
- Признак: $MONK$ - плоскость угла: $AD\parallel MONK$ и $BC\parallel MONK$
Алгоритм: вычисление угла в пространстве или плоскости
- В каком треугольнике этот угол? узнать стороны треугольника и найти угол по теореме косинусов.
- Если треугольник окажется равнобедренным, то провести высоту и найти угол прямоугольного треугольника.
- А если треугольник прямоугольный, то написать cos или sin или tg этого угла и найти как arc !
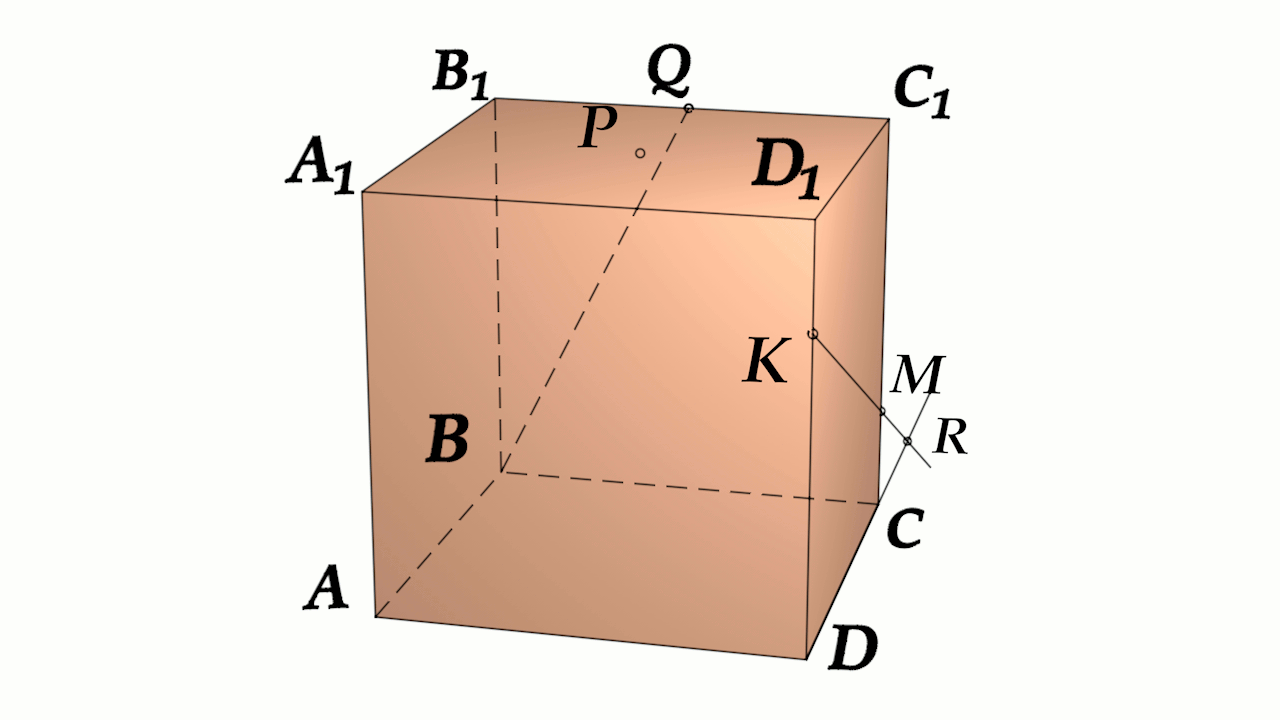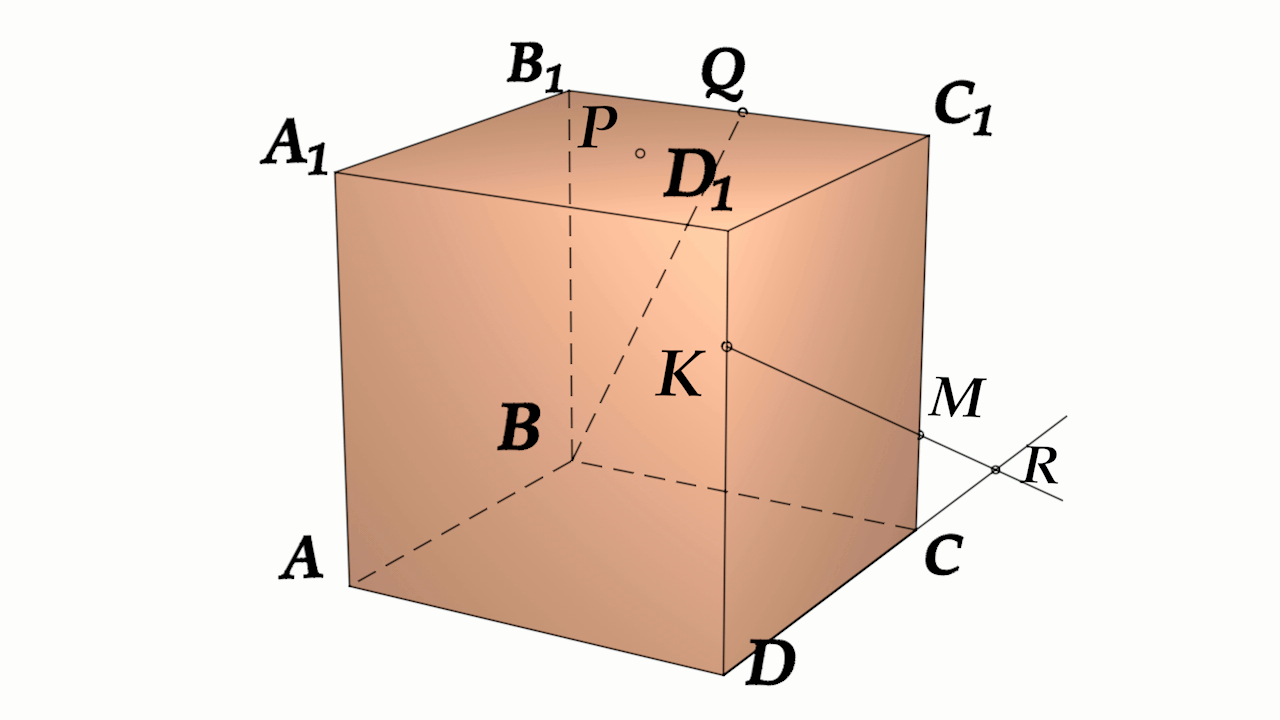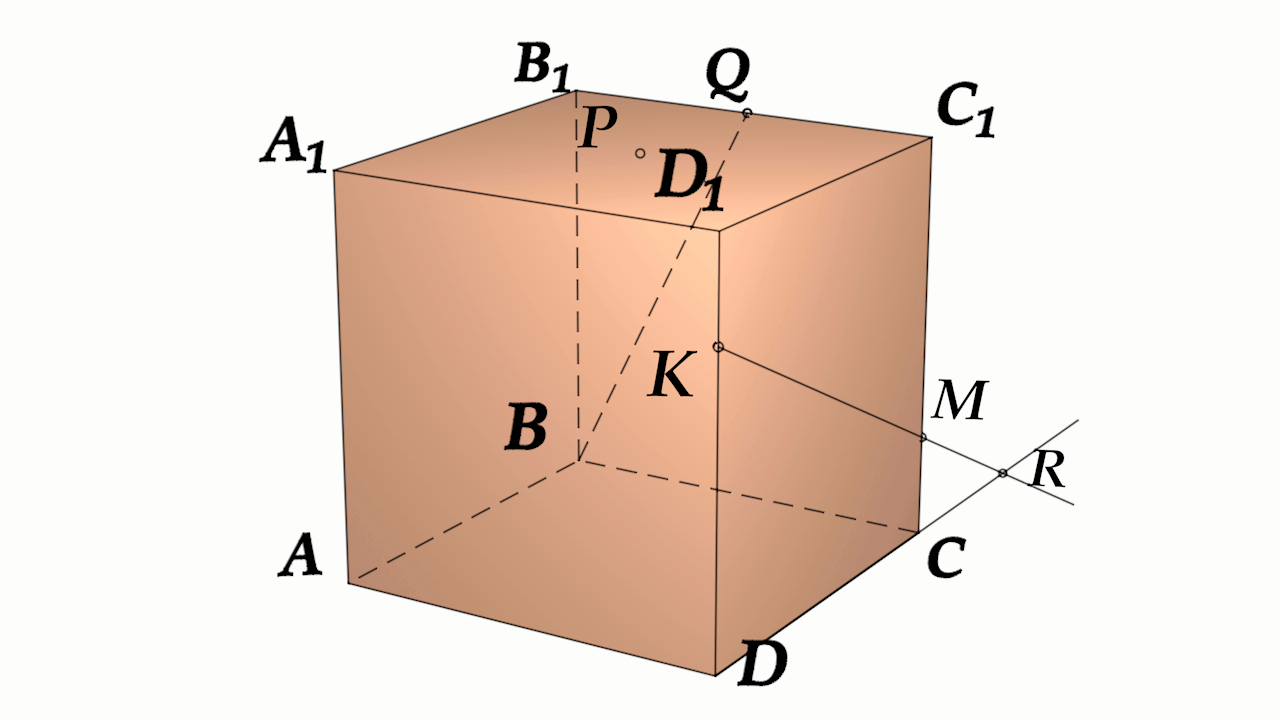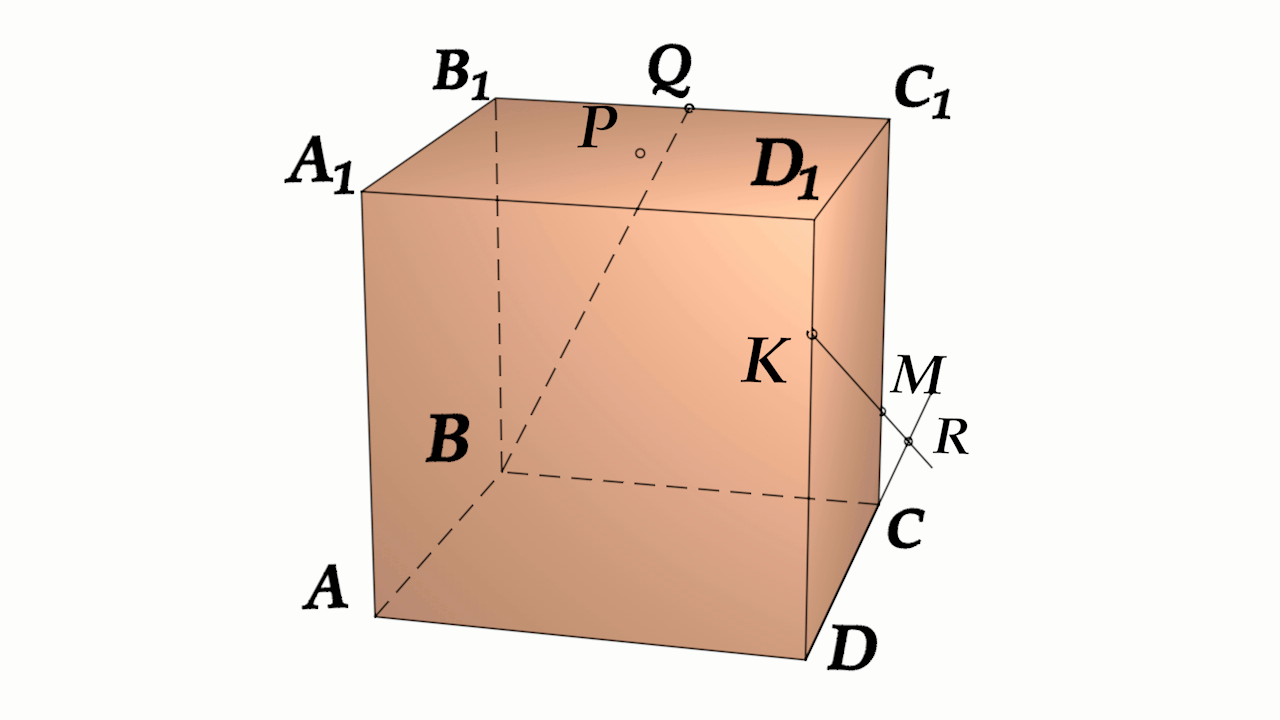
Задача 4: В кубе $ABCD{A_1}{B_1}{C_1}{D_1}$ все ребра равны $1$. Точка $Q$ - середина ребра . Точка $K$ делит ребро $D_1D$ в соотношении $1 : 3$ считая от вершины $D_1$, а точка $M$ делит $C_1C$ в соотношении $5 : 2$ считая от вершины $C_1$. (a) Найти угол между скрещивающимися прямыми $BQ$ и $KM$ . (b) Найти расстояние м\ж скрещивающимися $AB_1$ и $MK$
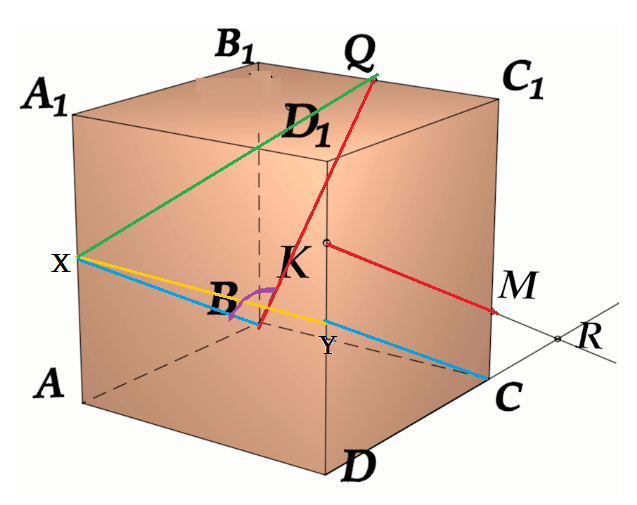
- (а) Параллельными переносами добъемся совмещения в точке $B$. Для этого, перенесем $KM$ в два этапа.
- Сперва соскользим $KM$ по грани $DD_1C_1C$ вдоль $C_1C$ до вершины $C$. Получим отрезок $CY\parallel MK$
- Затем, $CY$ протащим параллельно себе вдоль пути $CB$ и перейдем к отрезку $BX\parallel CY$.
- В итоге получили то, что надо: $KM$ параллельна $BX$, потому как $MK\parallel CY\parallel BX$.
- Требуемый угол $\angle \left(MK;BQ\right)=\angle \left(BX;BQ\right)=\angle XBQ$. Найдем его через треугольник $\bigtriangleup XBQ$
- В теореме косинусов нам нужны стороны этого треугольника. Вычислим постепенно, шаг за шагом, зная ребро куба 1:
- Из отношения $\frac{D_1K}{DK}=\frac{1}{3}\Rightarrow D_1K=\frac{1}{4}\ DK=\frac{3}{4}$. Из отношения $\frac{C_1K}{CM}=\frac{5}{2}\Rightarrow C_1M=\frac{5}{7}\ CM=\frac{2}{7}$
- $MK\parallel CY\Rightarrow KY=MC$ отрезок $DY=D_1D-D_1K-KY=1-\frac{1}{4}-\frac{2}{7}=\frac{13}{28}$
- $BX\parallel CY\Rightarrow BX=DY=\frac{13}{28}$. По условию задачи $B_1Q=\frac{1}{2}$.
- Нужные нам стороны треугольника $\bigtriangleup XBQ$ являются гипотенузами прямоугольных треугольников.
- Зная все катеты, как части ребер, по теореме Пифагора найдем стороны $XB$, $BQ$, $XQ$.
- Нужный угол $\angle XBQ$ вычислим из теоремы косинусов $XQ^2=XB^2+BQ^2-2\cdot XB\cdot BQ\cdot \cos \angle XBQ$
- наконец: $\cos \angle XBQ=\frac{XB^2+BQ^2-XQ^2}{2\cdot XB\cdot BQ}$ $\angle XBQ=\arccos \frac{XB^2+BQ^2-XQ^2}{2\cdot XB\cdot BQ}$
- Признак: $XBQ$ - плоскость угла: $KM\parallel XBQ$ и $BQ\in XBQ$
- (b Расстояние м\ж скрещивающимися $AB_1$ и $MK$ определим через параллельные плоскости, их содержащие.
- $AB_1$ находится на грани $AA_1B_1B$, $MK$ находиться на грани $DD_1C_1C$.
- Эти плоскости, $AA_1B_1B$ и $DD_1C_1C$ , суть те самые параллельные плоскости, содержащие наши скрещивающиеся $AB_1$ и $MK$.
- Расстояние $\bigtriangleup (AB_1;MK)=\bigtriangleup (AA_1B_1;DD_1C_1)=AD=1$ Ответ: $\bigtriangleup (AB_1;MK)=1$
Задача 5: В правильной треугольной призме $ABCMNK$ все ребра равны $2$. Точка $D$ делит ребро $MN$ в отношении $3 : 2$ считая от вершины $M$. a) Найдите угол между прямыми $AD$ и $BK$. b) Найти расстояние между прямыми $AM$ и $BK$
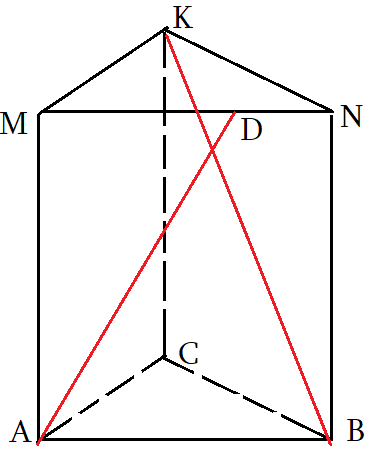
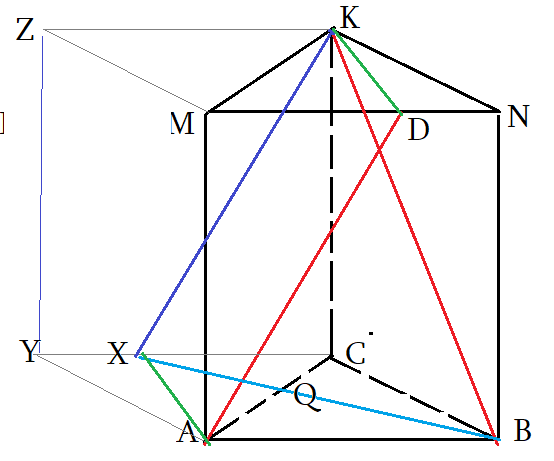
- (a) Чтоб найти угол между скрещивающимися прямыми, нужно "подвигать параллельно" $AD$ и $BK$ до совмещения.
- Если двинуть $AD$ так, чтоб точка $D$ совпала с $K$ - т.е. скользить по плоскости $ADK$, но тогда другой конец $D$ вне рисунка.
- Достроим призму до параллелепипеда $ABCYMNKZ$ и все нужные отрезки, "движения", плоскости будут внутри!
- $AD$ скользит по плоскости $ADK$ и совпадет с $XK$. Точка $X$, конечно, окажется на ребре $YC$
- по построению: $X\in CDK$ плоскости; $AD\parallel XK$ , $XC\parallel AB$ . Значит, $XK$ параллельна $AD$
- Угол между прямыми $\angle \left(AD;BK\right)=\angle \left(XK;BK\right)=\angle XKB$. Надо найти угол $\angle XKB$.
- Угол $XKB$ ищем , как обычно, через треугольник $\bigtriangleup XKB$, с помощью теоремы косинусов.
- Для этого надо найти стороны этого треугольника. Сторону $BK$ найдем по Пифагору для треугольника $\bigtriangleup BKC$.
- $XC=MD$, найдем $MD$ из отношения 3 : 2 для $MN$ . Затем, по Пифагору $\bigtriangleup XKC$ найдем $XK$.
- С вычислением $XB$ придется повозится через теорему косинусов треугольника $\bigtriangleup XBC$, две его стороны известны.
- А что с углом $\angle XCB$? по условию $\bigtriangleup ABC$ равносторонный, значит в параллелограмме $\angle YCB=120$ градусов.
- Ну и финально: как только найдем все стороны $\bigtriangleup XKB$, мы найдем и его угол $\angle XKB$ - то что надо!
- Признак: $XKB$ - плоскость угла: $AD\parallel XKB$ и $BK\in XKB$
- (b) Находим расстояние м\ж скрещивающимися $\bigtriangleup (AM;BK)$ через перпендикулярную плоскость:
- Плоскость основания $ABC$ перпендикулярна ребру $AM$. Она и есть перпендикулярная плоскость. Спроецируем скрещивающиеся ...
- Проекция $AM$ на $ABC$ - точка $A$ . Проекция $BK$ на $ABC$ - прямая $BC$ . Найдем расстояние м\ж проекциями.
- $\bigtriangleup (A;BC)=h_{ABC}$ - расстояние между проекциями скрещивающихся прямых равно высоте $\bigtriangleup ABC$.
- $\bigtriangleup (AM;BK)=\bigtriangleup (A;BC)=AB\cdot \frac{\sqrt{3}}{2}=\sqrt{3}$. Ответ: $\bigtriangleup (AM;BK)=\sqrt{3}$
Задача 6: $ABCA_1B_1C_1$ – правильная треугольная призма; все ее ребра равны $1$. расстояние $\rho $ между прямыми $AB$ и $CA_1$.
- $AB$ и $CA_1$ – скрещивающиеся прямые. Чтобы найти расстояние между ними, используем метод перпендикулярной плоскости.
- К прямой $AB$ все прямые ребра перпендикулярны.
- а) пусть $M$ и $M_1$ – середины $AB$ и $A_1B_1$. Тогда $MC$ – гипотенуза, высота, биссектриса в равнобедренном $\bigtriangleup ABC$.
- $MM_1\parallel CC_1$, $AB\perp CC_1$ $AB\perp MM_1$: Значит, $AB$ – перпендикуляр к двум пересекающимся прямым.
- А значит, $AB$ перпендикуляр и ко всей плоскости $AB\perp MM_1C_1C$.
- Метод Перпенд Плоскости: ищем расстояние м/д проекциями $AB$ и $A_1C$ на перпендикулярную $MM_1C_1C$ плоскость....
- Найдем проекции $AB$ и $A_1C$ на $MM_1C_1C$: Проекция $AB$ - точка $M$ .
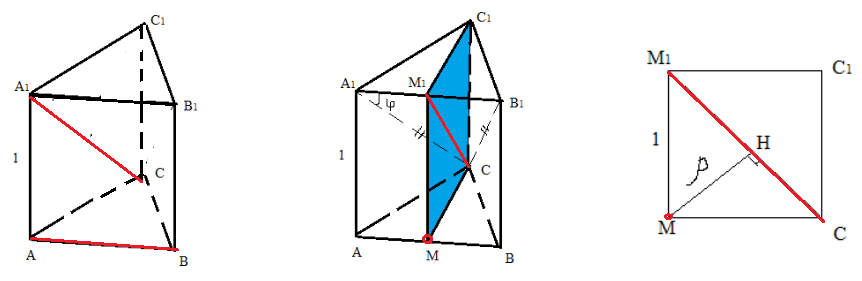
- Спроектируем прямую $A_1C$ на плоскость, его концы: Точка $C$ уже лежит в этой плоскости.
- Необходимо найти проекцию, перпендикуляр от точки $A_1$ к плоскости $MM_1C_1C$.
- $AB$ перпендикуляр к этой плоскости, $A_1M_1$ – перпендикуляр к плоскости;
- $M_1$ проекция точки $A_1$ на плоскость. Прямая $A_1C$ проектируется на плоскость в прямую $M_1C$. .
- Теперь нужно найти расстояние м\ж проекциями прямых: - расстояние от точки $M$ до прямой $M_1C$.
- Искомое расстояние $rho$ это высота, опущенная из прямого угла в прямоугольном $\bigtriangleup M_1MC$:
- По построению имеем перпендикулярности: $MH\perp M1C$ , значит $MH\perp A1CB1$. также $MH\perp AB$.
- Значит: $MH$ нужное расстояние м/д $AB$ и $A1CB1$.
- $MM1=AA1=1$ $MC$ высота в равностороннем $\bigtriangleup ACB$ $MC=M1C1=AC\sin 60=\frac{\sqrt {3}}{2}$
- $M1C=\sqrt {1^2+(\frac{\sqrt {3}}{2})^2}=\frac{\sqrt {7}}{2}$ $\rho=\bigtriangleup (M;M_1C)=MH$ $\rho=MM_1\cdot \sin \angle MM_1C=1\cdot \frac{MC}{M_1C}= \frac{\frac{\sqrt {3}}{2}}{\frac{\sqrt {7}}{2}}=\frac{\sqrt {3}}{7}$
- Ответ: расстояние $\rho$ между прямыми $AB$ и $CA_1$ равно $\frac{\sqrt {3}}{7}$
Метод параллельной плоскости,* расстояние от прямой до параллельной плоскости:
- Имеем две скрещивающиеся прямые. Строим плоскость, которая содержит прямую и параллельна второй прямой.
- Как? параллельный сдвиг: вторую прямую параллельно перетащим до пересечения с первым прямым.
- Расстояние от второй прямой до построенной параллельной плоскости есть искомое расстояние м\ж скрещивающимися ....
- факт: расстояние от прямой до параллельной с ним плоскоскости равен рсстоянию от любой точки прямой до плоскости.
- Расстояние м\ж крещивающимися прямыми то же самое,что расстояние м\ж их параллельными плоскостьтями!
Метод перпендикулярной плоскости, расстояние между проекциями скрещивающихся прямых:
- Имеем две скрещивающиеся прямые. Находим плоскость, которая перпендикулярна первой прямой.
- Проектируем скрещивающиеся прямые на эту плоскость. Проекция первой – точка!
- Находим проекцию 2-ой прямой: проектируем его две точки, опуская перпендикуляры на плоскость. Соединим.
- Находим расстояние от проекции-точки до проекции-прямой: это и есть кратчайшее м\д скрещивающимися.
Упражнения: