Функция $y=\frac{k}{x}$ . Гипербола. Свойства.
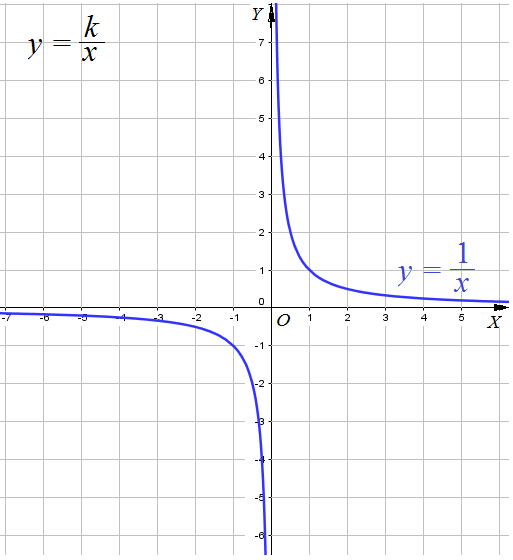
Пример 1: Построить график для функции $y=\frac{1}{x}$, $f\left(x\right)=\frac{1}{x}$
- Вычислим значения функции в разнознаковых точках и нанесем точки с вычисленными координатами в системе $XOY$.
- $x=1$ $f\left(1\right)=1$ $x=\frac{1}{2}$ $f\left(\frac{1}{2}\right)=2$ $x=-1$ $f\left(-1\right)=-1$ $x=-\frac{1}{2}$ $f\left(-\frac{1}{2}\right)=-2$
- $x=2$ $f\left(2\right)=\frac{1}{2}$ $x=\frac{1}{4}$ $f\left(\frac{1}{4}\right)=4$ $x=-2$ $f\left(-2\right)=-\frac{1}{2}$ $x=-\frac{1}{4}$ $f\left(-\frac{1}{4}\right)=-4$
- $x=4$ $f\left(4\right)=\frac{1}{4}$ $x=\frac{1}{8}$ $f\left(\frac{1}{8}\right)=8$ $x=-4$ $f\left(-4\right)=-\frac{1}{4}$ $x=-\frac{1}{8}$ $f\left(-\frac{1}{8}\right)=-8$ .
- В системе координат укажем точки $(1;1)$, $(2;1/2)$, $(4;1/4)$, $(1/2;2)$, $(1/4;4)$, $(1/8;8)$, $(-1;-1)$, $(-2;-1/2)$,
- Еще точки: $(-4;-1/4)$, $(-1/2;-2)$, $(-1/4;-4)$, $(-1/8;-8)$ . По всем точкам построим кривые - график функции $y=\frac{1}{x}$
- Функция $y=\frac{1}{x}$ не вычисляется при $x=0$, О.Д.З. $x\ne0$ . График имеет разрыв по вертикальной линии $x=0$. Ветви "прижаты" к ней.
- Ветви графика прижимаются к горизонтальной линии $y=0$. Функция $y=\frac{1}{x}$ ни при каких $x$ не принимает значение $y=0$
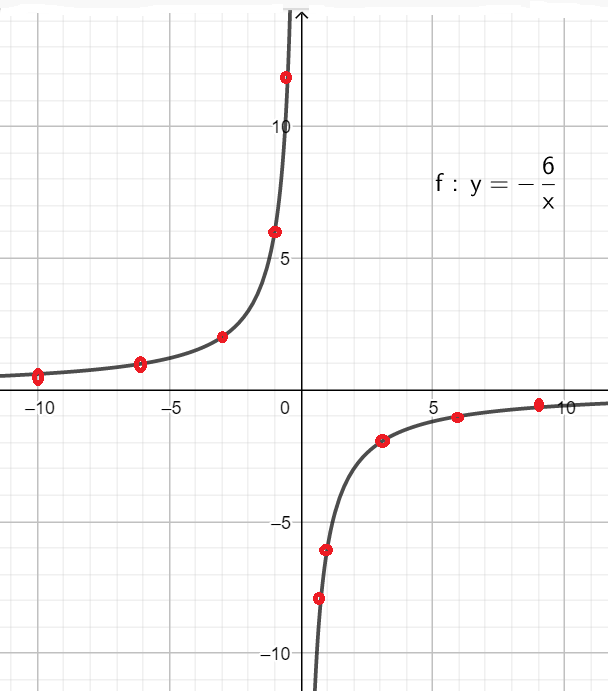
Пример 2: Построить график для функции $y=-\frac{6}{x}$, $f\left(x\right)=-\frac{6}{x}$
- Вычислим значения функции в разнознаковых точках и нанесем точки с вычисленными координатами в системе $XOY$.
- $x=1$ $f\left(1\right)=-6$ $x=\frac{1}{2}$ $f\left(\frac{1}{2}\right)=-12$ $x=-1$ $f\left(-1\right)=6$ $x=-\frac{1}{2}$ $f\left(-\frac{1}{2}\right)=12$
- $x=2$ $f\left(2\right)=-3$ $x=\frac{3}{4}$ $f\left(\frac{3}{4}\right)=8$ $x=-2$ $f\left(-2\right)=12$ $x=-\frac{3}{4}$ $f\left(-\frac{3}{4}\right)=8$
- $x=4$ $f\left(4\right)=-1,5$ $x=6$ $f\left(6\right)=-1$ $x=-4$ $f\left(-4\right)=1,5$ $x=-12$ $f\left(-12\right)=-0,5$ .
- В системе координат укажем точки $(1;-6)$, $(2;-3)$, $(4;-1,5)$, $(1/2;-12)$, $(3/4;-8)$, $(-2;3)$, $(-1;6)$, $(-3;2)$,
- Еще точки: $(-4;1,5)$, $(-1/2;12)$, $(12;-0,5)$, $(-12;0,5)$ . По всем точкам построим кривые - график функции $y=\frac{1}{x}$
- Функция $y=-\frac{6}{x}$ не вычисляется при $x=0$, О.Д.З. $x\ne0$ . График имеет разрыв по вертикальной линии $x=0$. Ветви "прижаты" к ней.
- Ветви графика прижимаются к горизонтальной линии $y=0$. Функция $y=-\frac{6}{x}$ ни при каких $x$ не принимает значение $y=0$
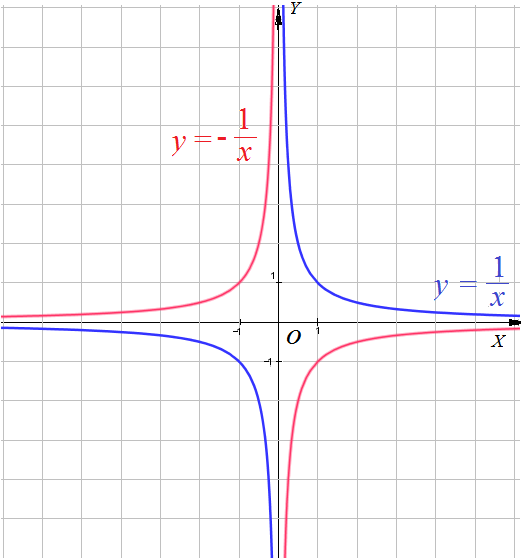
Графиком функции $y=\frac{k}{x}$ $k\ne0$ является гипербола , ветви прижимаются к асимптотическим линиям.
- если коэффициент $k > 0$ , в I и III координатных четвертях. Точка $(0;0)$ - центр симметрии.
- если $k < 0$ , то во II и IV координатных четвертях. Точка $(0;0)$ - центр симметрии.
- Асимптоты: Вертикальная асимптота, линия $x=0$, Горизонтальная асимптота, линия $y=0$
Cвойства функции $y=\frac{k}{x}$ при $k > 0$ ( ветви гиперболы расположены в первом и третьем координатных углах) .
- Свойство 1: Область Определения Функции - вся числовая прямая , кроме $x=0$.
- Свойство 2: $y > 0$ при $x > 0$; $y < 0$ при $x < 0$.
- Свойство 3: Функция убывает на промежутках $( - ∞ ; 0 )$ и $( 0 ; + ∞)$
- Свойство 4: Функция не ограничена ни снизу, ни сверху.
- Свойство 5: Ни наименьшего, ни наибольшего значений $у$ функций нет.
- Свойство 6: Функция непрерывна на $( - ∞ ; 0 )$ и $( 0 ; + ∞)$.
- Свойство 7: Область значений функции - $( - ∞ ; 0 )$ U $( 0 ; + ∞)$. имеет разрыв в точке $x=0$.
Cвойства функции $y=\frac{k}{x}$ при $k < 0$ (ветви гиперболы расположены во втором и четвертом координатных углах).
- Свойство 1: Область Определения Функции - вся числовая прямая , кроме $x=0$.
- Свойство 2: $y > 0$ при $x < 0$ ; $y < 0$ при $x > 0$.
- Свойство 3: Функция возврастает на промежутках $( - ∞ ; 0 )$ и $( 0 ; + ∞)$
- Свойство 4: Функция не ограничена ни снизу, ни сверху.
- Свойство 5: Ни наименьшего, ни наибольшего значений $у$ функций нет.
- Свойство 6: Функция непрерывна на $( - ∞ ; 0 )$ и $( 0 ; + ∞)$
- Свойство 7: Область значений функции - объединение $( - ∞ ; 0 )$ U $( 0 ; + ∞)$ . имеет разрыв в точке $x=0$.
Графический способ решения уравнений
Пример 3: Решить уравнение $\frac{2}{x}=x^2+1$ графическим способом.
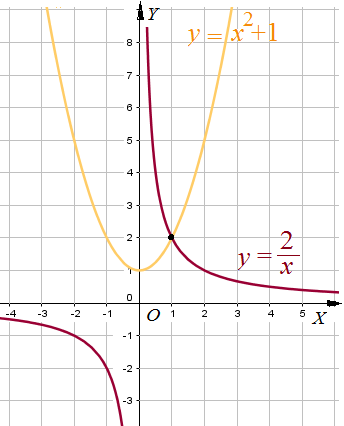
- Рассмотрим две функции : $y=\frac{2}{x}$ и $y=x^2+1$ построим гиперболу $y=\frac{2}{x}$ и параболу $y=x^2+1$ по
- чертежу видно, что графики пересекаются в точке с координатами $\left(1;2\right)$. если подставить $x=1$ в уравнение,
- то равенство выполняется: $\frac{2}{1}=1^2+1$ обе функции принимают одно и то же значение $2=2$.
- ответ: $x=1$. при таком $x$ графики пересекаются.
- "почему?": при каких $x$ - числах выравнываются обе части уравнения? при тех $x$ - числах, при которых левая
- функция и правая функция приобретают одинаковые значения ... это то же самое, что графики этих функций
- пересекаются в точках с такими $x$ - координатами.
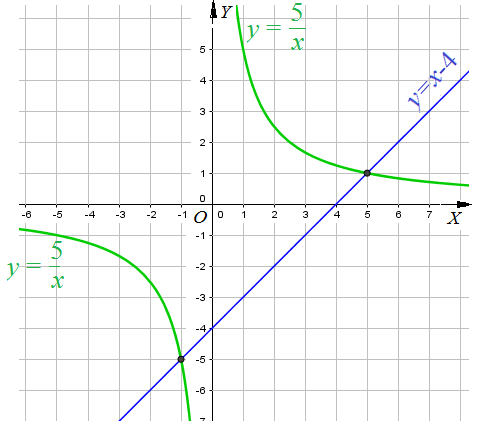
Пример 4: Решить уравнение $\frac{5}{x}=x-4$.
- рассмотрим две функции: $y=\frac{5}{x}$ и $y=x-4$, построим их графики: гиперболу $y=\frac{5}{x}$ и прямую $y=x-4$.
- по чертежу видно, что гипербола и прямая пересекаются в точках $(-1;-5)$ и $(5;1)$. проверим, подставим
- $x=-1$ и $x=5$ в уравнение : $\frac{5}{-1}=-1-4$ $\Leftrightarrow$ $-5=-5$ и $\frac{5}{5}=5-4$ $\Leftrightarrow$ $1=1$ . равенство
- выполняется, значит данное уравнение имеет два корня - абциссы точек пересечения графиков.
- ответ: $x_1=-1$; $x_2=5$.
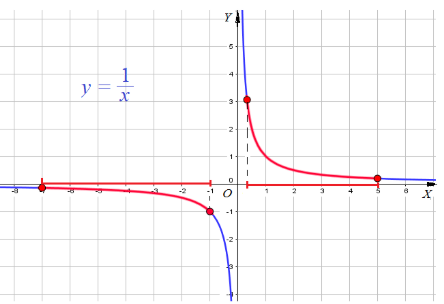
Пример 5: Найти наименьшее и наибольшее значения функции $y=\frac{1}{x}$ на отрезках а) $\left[\frac{1}{3};5\right]$ и б) $\left[-7;-1\right]$.
- Построим график функции $y=\frac{1}{x}$ .
- Выделим часть графика, соответствующую значениям переменной $x$ на отрезке $\left[\frac{1}{3};5\right]$.
- Для выделенной части графика находим: наименьшее значение $y=\frac{1}{5}$ при $x=5$ , наибольшее $y=3$ при $x=\frac{1}{3}$.
- Оформление: $\left[\frac{1}{3};5\right]$ $f\left(5\right)=\frac{1}{5}$ $f\left(\frac{1}{3}\right)=3$
- Выделим часть графика, соответствующую значениям переменной $x$ на отрезке $\left[-7;-1\right]$.
- Для выделенной части графика находим: наименьшее значение $y=-\frac{1}{7}$ при $x=-7$ наибольшее $y=-1$ при $x=-1$.
- Оформление: $\left[-7;-1\right]$ $f\left(-7\right)=-\frac{1}{7}$ $f\left(-1\right)=-1$
Пример 6: Доказать, что функция $y=f\left(x\right)$ , где $f\left(x\right)=\frac{4}{x}$
удовлетворяет соотношению $f\left(x-5\right)-f\left(x+1\right)=1,5\cdot f\left(x-5\right)\cdot f\left(x+1\right)$.
- Подставим в аргументы функций значения $x-5$ и $x+1$, получим: $f\left(x-5\right)=\frac{4}{x-5}$ и $f\left(x+1\right)=\frac{4}{x+1}$ .
- распишем левую часть тождества $f\left(x-5\right)-f\left(x+1\right)=\frac{4}{x-5}-\frac{4}{x+1}=\frac{4\left(x+1\right)-4\left(x-5\right)}{\left(x-5\right)\left(x+1\right)}=\frac{24}{\left(x-5\right)\left(x+1\right)}$. аналогично,
- с правой стороны получим $1,5\cdot f\left(x-5\right)\cdot f\left(x+1\right)=1,5\frac{4}{x-5}\cdot\frac{4}{x+1}=\frac{1,5\cdot16}{\left(x-5\right)\left(x+1\right)}=\frac{24}{\left(x-5\right)\left(x+1\right)}$. одинаковые! ч.т.д.
Упражнения:
