I.       Сколько пересечений у            $y=f\left(x\right)$      с       $y=m$   или     $y=kx$

Постройте график функции . Определите, при каких значениях k прямая y = kx имеет с графиком ровно одну общую точку.

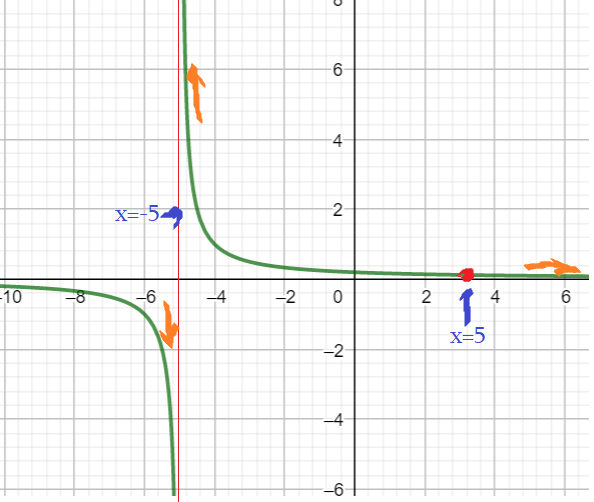
Задача 1:                Дан график функции     $y=\frac{x-5}{x^2-25}$   .   При каком    $m$    этот график не пересекается с графиком   $y=m$ . При каком   $k> 0$     это график пересекается с графиком    $y=kx$   ровно один раз.

• $m$ какое то число. Поэтому, график функции   $y=m$ горизонтальная линия, проходящая в точке   $(0;m)$, на ординате $m$.
• Какая горизонтальная прямая пересекается с нашим графиком ровно один раз?   Посмотрим график   функции     $y=\frac{x-5}{x^2-25}$.
• Визуально видно, что горизонтальная прямая   $y=m$, не пересекающая наш график, должен "протиснуться" в выколотой точке $(5;0,1)$ или ...
• $m=0$ тоже ни разу не персекает, т.к. она горизонтальная асимптота!    Внимание: для всех остальных    $y=m$ хотя бы раз пересекает.
• Понятно, что в   выколотой точке $(5;0,1)$   проходит если только    $m=0,1$.       ответ:      $m=0$   или    $m=0,1$.
• Прямые    $y=kx$   "крутятся" вокруг начала координат   $(0;0)$. Если   $k> 0$ то, эти прямые находятся в I-ой III-ей четвертях.
• Какой из них только раз пересекается с графиком   $y=\frac{x-5}{x^2-25}$ ? Тут две гиперболы. Прямая должна пройти в выколотой точке.
• Прямая    $y=kx$, проходящая в точке   $(5;0,1)$ должен иметь такое   $k$, чтобы   $0,1=k\cdot5$   $\Rightarrow$       ответ:    $k=0,02$

                      

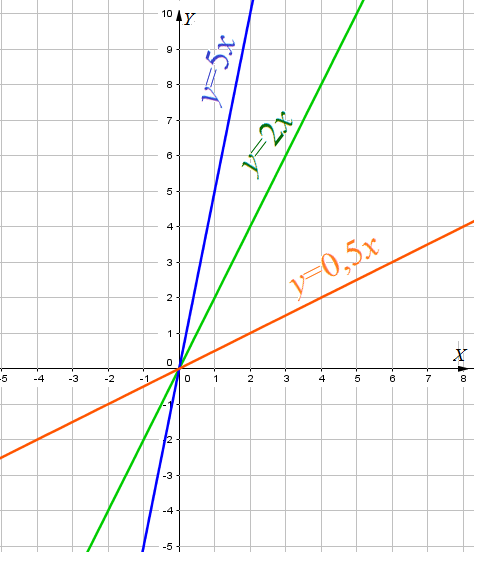
Прямая имеет с графиком ровно одну общую точку либо тогда, когда проходит через вершину параболы, либо тогда, когда пересекает параболу в двух точках, одна из которых  — выколотая.   

Прямая линия    $y=kx$ - вращается вокруг начало координат   $(0;0)$.      $k$ коэффициент   наклона

Прямая линия    $y=m$ - движется горизонтально, параллельно абсциссе, на уровне   "ордината $= m$."

• Когда,    при каком значении параметра,    прямая проходит точку $(-5;-3)$ ?
• вращающаяся    $y=kx$:    проходит $(-5;-3)$ ?        $\Rightarrow$     $-3=k \cdot (-5)$      .
• горизонтальная   $y=m$:    проходит $(-5;-3)$ ?       $\Rightarrow$     $-3=m$   
  
• При каких значения параметра    прямая   пересекает график   функции $y=f\left(x\right)$   два раза?
• $y=kx$   вращаем вокруг   $(0;0)$ . Ищем ситуации "пересекает 2 раза". С учетом "дыр, выколотых точек".
• $y=m$ двигаем горизонтально и ищем "пересекает 2 раза". Уточняем значения параметров в нужных ситуациях.

Вопросы одинакового смысла - эквивалентные утверждения:

• При каком значении параметра     $k$     графики        $y=\frac{9-x^2}{2x-5}$      и   $y=kx$     имеют две общие точки?
• При каком значении параметра     $k$     прямая      $y=kx$     пересекает график      $y=\frac{9-x^2}{2x-5}$      два раза?
• При каком значении параметра     $k$     уравнение      $\frac{9-x^2}{2x-5}=kx$       имеет два различных решения?
• Одно и то же:    "Нет общих точек"        =         "Нет пересечений графиков"         =         "Нет решений уравнения"

Алгоритм:     Квадратичная   функция     $y=ax^2+bx+c$. Ее график - Парабола.    

• 1-ая точка графика:      Вершина параболы находится при    $x=-\frac{b}{2a}$.   Там $min/ max$ !     Координаты   вершины     $\left(-\frac{b}{2a};\frac{4ac-b^2}{4a}\right)$.
• Ось симметрии параболы - вертикальная линия через Вершину .     Еще точка   $(0;c)$     даст пересечение   с   осью   $Y$.
• Вычислим функцию еще в двух-четырех точках, на одинаковом расстоянии от вершины     $x=-\frac{b}{2a}\pm3$   или $x=-\frac{b}{2a}\pm4$ .

II.       Кусочные функции,    .... параметры

Функция на 3-х интервалах:        $y=x-0,5$   при $x<-2$         $y=-2x-6,5$   при $-2\le x\le-1$        $y=x-3,5$ при   $x>-1$

• Особые точки сломов-склеиваний кусков функции:.            $x=-2$          $x=-1$   
  
• Строим график $y=x-0,5$.   Оставляем ее часть на интервале   $(-\infty;-2)$.     остальное стираем за ненадобностью.
• Строим   $y=-2x-6,5$ и оставляем из интервала $-2\le x\le-1$.    Прямую   $y=x-3,5$   оставляем лишь на $x>-1$.
• Склеиваем три куска , каждое на своем интервале. Получим график   Кусочной функции.
• Двигаем горизонтальные   $y=m$: Смотрим разные    $m=-7$,     $m=-4,5$,     $m=-3$,   $m=-2,5$,   $m=-1$,   $m=2$,    $m=5$.
• При конктретном   $m=?$ главный вопрос: сколько пересечений с графиком, сколько общих точек?

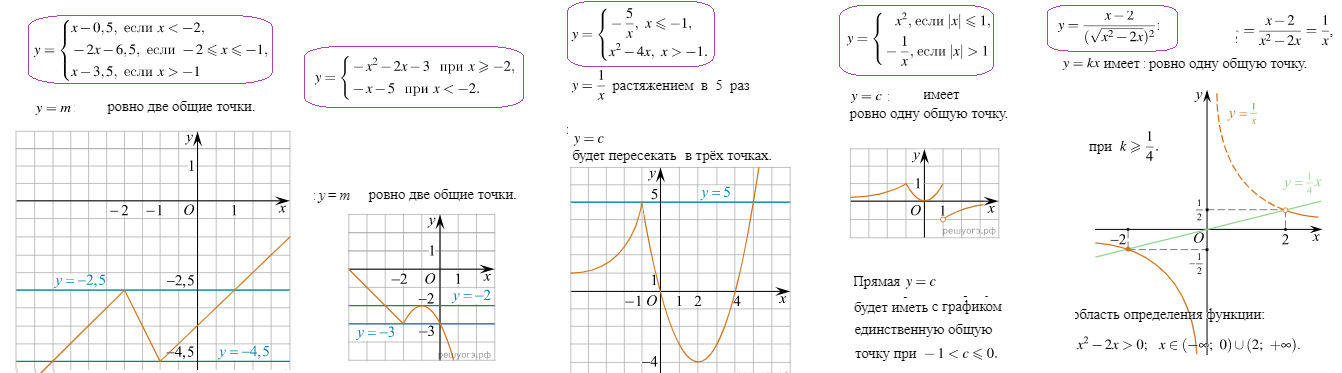
• 2-ая функция: склеивание в точке $(-2;-3)$. Слева кусок прямой, справо кусок - часть параболы.
• Парабола имеет вершину в точке $(-1;-2)$.      Формула вершины параболы:    $x=-\frac{b}{2a}$
• 3-ая функция:      слева гипербола и справа парабола склеиваются в "сломе"     $(-1;5)$
• Два пересечения с $y=c$, два корня получаются лишь при прохождении "слома", т.е.   $c=5$.
• 4-ая функция:    имеет "сломы" при $\left|x\right|=1$.   Т.е. при   $x=-1$   и   $x=1$
• На интервале    $-1<x<1$   оставляем кусок параболы.   Вне слева и справа куски гиперболы.
• При этом для $x=1$ надо брать значение от гиперболы, из-за условий функций. Поэтому, там     разрыв!
• 4-ая функция:      Из-за ОДЗ радикала выпадает интервал $(0;2)$. В нем функция   не существует!
• Поэтому, часть гиперболы на интервале   $(0;2)$ должно быть вычеркнуто. Там нет функции.
• Когда вращающаяся    $y=kx$: пересекает один раз полученный график?
• Как раз там, где он пересекал бы   вычеркнутый кусок гиперболы!:
• Надо понять где этом момент начинается: - при каком   $k$   прямая   $y=kx$ проходит точку    $(2;0,5)?$

III.      Графики функций с модулями,    .... параметры

Модуль $\left|A\right|=A$   выражения $A>0$   равен          $\left|A\right|=A$   если   $A\ge0$ ;    $\left|A\right|=-A$    если $A<0$

• Т.е.   модуль    где-то равен "+" подмодульному , а в других местах     "-" подмодульному
• В зависимости от знака подмодульного выражения .    Поэтому важно узнать при каких $x=?$   подмодульное обнуляется
• Составить уравнение подмодульное = 0 ,решить его и получить интервалы для раскрытия модуля.

Как и на каких интервалах раскрывать модули для функции с модулями? По критическим точкам!

• Функция с модулями на одних интервалах равна одной функции, на других - другой. В зависмости где как раскрывается модуль.
• Для верного раскрытия модулей надо установить все критические точки функции (КТ):
• Для каждого модуля составляем уравнение    подмодульное = 0     и его решения дадут КТ.
• Для каждой дроби составляем уравнение    знаменатель = 0     и его решения будут КТ.
• Для каждого квадратного радикала составляем уравнение    подрадикальное = 0     и его решения дадут КТ.
• Расположим все полученные критические точки в порядке возрастания. Получим разбиение числовой оси на интервалы.
• На каждом интервале путем вычисления пробной точки выясняем знак подмодульного и с этим знаком раскрываем модуль!

• Как построить график 2-ой функции: с модулем      $y=x^2-\left|8x+3\right|$ ?
• Слом    там, где подмодульное выражение обнуляется:      $8x+3=0$    $\Rightarrow$ точка слома $x=-\frac{3}{8}$.
• Левее от   $x=-\frac{3}{8}$ модуль раскрывается со знаком "-" , а правее от нее модуль = () со знаком "+"
• Функция с модулем превращается    в кусочную    из двух склеивающихся парабол.
  
• Важные, особые точки:    слом и вершины парабол, $x=-\frac{3}{8}$, $x=-4$,   $x=-4$. Вычислим значения функции в них!
• 3-ая функция: имеет критическую точку   $x=3$. Левее от нее модуль раскрывается с знаком "-", т.е. $\left|x-3\right|=-(x-3)$
• Для 1-ой функции еще проще: модуль левее слома   $x=0$   равен      $-(x)$,     а правее      $+(x)$

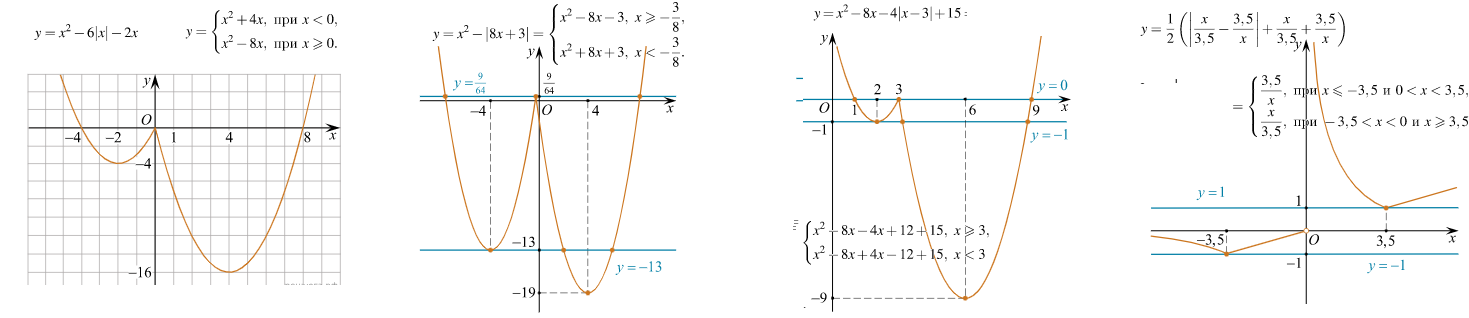
• Для 4-ой функции: составляем критические уравнения:   $\frac{x}{3,5}-\frac{3,5}{x}=0$   и $x=0$. Получим точки   $-3,5<0<3,5$
• На интервалах   $(-\infty;-3,5)$   и   $(0;3,5)$   подмодульное отрицательно, поэтому модуль раскрывается как "-". Гипербола!
• На интервалах   $(-3,5;0)$   и   $(3,5;+\infty)$ подмодульное положительно, раскрытие "+". Итоговая функция - линейная.
• Строим графики: гиперболу    $\frac{3,5}{x}$   и прямую   $\frac{x}{3,5}$.    Но оставляем куски лишь "своих интервалов".
• Важно: четко вычислить координаты всех особых точек!       "слома",      "склеивания",    "переходов",   "обнуления под ..."

IV.       Графики с выколотыми точками, сокращения, ОДЗ.    .... параметры

Как построить график дробной функции с сокращением, "выколотыми точками"

• Для 1-ой функции:           $y=\frac{x^4-13x^2+36}{\left(x-3\right)\left(x+2\right)}$            проведем "процедуру безопасного сокращения":
  
• Самое главное,   ОДЗ:       $x-3\ne0$,    $x+2\ne0$.   В функции, в уравнениях точки    $x=3$,    $x=-2$     под запретом!
• Для сокращений используем формулы разложения:     Виета      $ax^2+bx+c=a\left(x-x_1\right)\left(x-x_2\right)$    сокращенное умножение       $a^2-b^2=\left(a-b\right)\left(a+b\right)$
• Биквадратное         $x^4-13x^2+36=t^2-13t+36=(t-9)(t-4)=(x^2-9)(x^2-4)=(x-3)(x+3)(x-2)(x+2)$.      
  
• Теперь, видим в числителе и знаменателе одинаковые    $(x-3)$    и    $(x+2)$   , можем сократить .   Помним ОДЗ!
• Наша функция стала новой     $y=(x+3)(x-2)$,   но без учета выколотых точек     $x\ne3$,    $x\ne-2$   из-за ОДЗ.
• Факт:   Функции и    $y=\frac{x^4-13x^2+36}{\left(x-3\right)\left(x+2\right)}$   ,     $y=(x+3)(x-2)$    и их графики совпадают всюду, кроме двух точек   $x=3$,    $x=-2$.
• При пересечении графика с прямыми типа   $y=m$   или     $y=kx$ учытиваем   прохождение через выколотые точки!

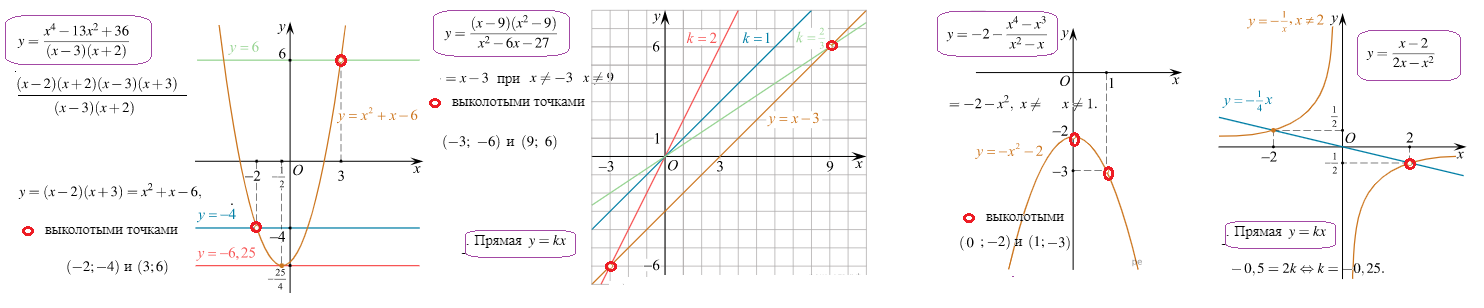
• 2-ая функция: совпадает с простой   $y=x-3$ всюду кроме ... вычислим   $x-3$ в них ... получим выколотые $(-3;-6)$ и   $(9;6)$.
• Вращающаяся $y=kx$ ни разу не пересекает график либо проскакивая через выколотые, либо когда параллельно! При каком   $k$?
• 3-ая функция: после сокращения превращается в параболу   $-x^2-2$   за исключением точек $0$ и $1$. Вычилислим в них!
• 4-ая функция: равна гиперболе с выколотыми!           При каком   $k$   прямая $y=kx$ пройдет через выколотое?

V.       Прочие функции,   задачи

Задача 2:         Найдите   $c$ и постройте график функции   $y=x^2+c$ ,    если известно, что прямая   $y=4x$   имеет с графиком ровно одну общую точку.

• Графики имеют одну общую точку     $\Leftrightarrow$     уравнение     $x^2+c=4x$   имеет одно решение     $\Leftrightarrow$    дискриминант = 0 ?   

Задача 3:         Найдите наименьшее значение выражения     $\left(5x-4y+3\right)^2+\left(3x-y-1\right)^2$    и значения    $x$   и   $y$,    при которых оно достигается.

• Сложение квадратов? наименьшее значение тогда, когда оба обнуляются!    Решаем систему    $5x-4y+3=0$   и   $3x-y-1=0$.

Задача 4:         При каких значениях p вершины парабол $y=x^2+4px-1$   и   $y=-x^2+6px-p$   расположены по разные стороны от оси $x$?

• Вершина первой по формуле    $x=-\frac{b}{2a}$    $x=-\frac{4p}{2}=-2p$. Значение    в нем   $y=(-2p)^2+4p(-2p)-1=-4p^2-1$
• Вершина второй параболы      $x=-\frac{-6p}{-2}=3p$ ,   значение       $y=-(3p)^2+6p(3p)-p=9p^2-p$
• Вершины будут по разные стороны от оси $x$      $\Leftrightarrow$    эти значения разного знака       $\Leftrightarrow$       $(-4p^2-1)(9p^2-p)>0$
  
• Решим неравенство. Учтем   $-4p^2-1$    всегда отрицательно. Уберем. Получим     $9p^2-p<0$     $\Rightarrow$    $9p\left(p-\frac{1}{9}\right)>0$

Задача 5:         Первая прямая проходит через точки      $(0; 4,5)$ и $(3; 6)$.     Вторая прямая проходит через точки    $(1; 2)$   и   $(-4; 7)$.    Найдите координаты общей точки этих двух прямых.

• 1-ая прямая, проходящая через    точки   $(0; 4,5)$ и $(3; 6)$     имеет уравнение    $\frac{y-4,5}{6-4,5}=\frac{x-0}{3-0}$
• 2-ая прямая проходит через точки   $(1; 2)$   и   $(-4; 7)$,      ее уравнение    $\frac{y-2}{7-2}=\frac{x-1}{-4-1}$
  
• Упростим оба:     $2y-9=x$      $y-2=1-x$ . Чтоб найти общую    точку, надо решить систему из двух неизвестных.

Если прямая проходит через две точки с координатами $(x_1;y_1)$ и     $(x_2;y_2)$

то уравнение прямой составляется так:       $\frac{y-y_1}{y_2-y_1}=\frac{x-x_1}{x_2-x_1}$

Задача 6:        Прямая    $y = 2x + b$ касается окружности      $x^2+y^2=5$    в точке с положительной абсциссой. Определите координаты точки касания.

• В точка касания   $(x;y)$ должна удовлетворять оба    равенства, т.е. систему    $y = 2x + b$ и    $x^2+y^2=5$. При этом   $x>0$
• Подставим первое во второе:     $x^2+(2x+b)^2=5$. Полученное уравнение должно иметь единственное    решение.
• Квадратное уравнение имеет единственное решение, если только дискриминант    равен нулю!
• $5x^2+4xb+b^2-5=0$    его дискриминант   $16b^2-4\cdot5\cdot\left(b^2-5\right)=0$    $\Rightarrow$    $-4b^2+100=0$    $\Rightarrow$    $b=5$ и $b=-5$
• При    $b=5$ найдем $x$   из    $5x^2+4xb+b^2-5=0$:   $5x^2+20x+20=0$ $\Rightarrow$ $x=-2$.    нет $x>0$ !
• При    $b=-5$ найдем $x$   из    $5x^2+4xb+b^2-5=0$:   $5x^2-20x+20=0$   $\Rightarrow$ $x=2$.   есть   $x>0$ !
• Условию с положительной    абсциссой $x>0$ удовлетворяет пара    $b=-5$ и   $x=2$. Тогда $y=2x + b=4-5$. Касание   $(2;-1)$

VI.       Сведения о графиках функций, свойства, построения

Прямоугольная система координат:      положение точки определяется двумя её координатами - абcциссой и ординатой .     (А)   Система   координат:       Абсцисса    -    ось   $x$.     Ордината     -    ось   $y$.     (В)   Точка $(2;-3)$:     пересечение линий:        горизонтальная   линия    $y = -3$ ;     (С)   вертикальная   линия      $x = 2$     (Д)   Точка   с   координатами   $(x;y)$    например,   $(2;-3)$ :   наносим точку, справа на   2   единицы, вниз на 3 единицы.

Алгоритм:    детальное построение   графика   заданной   функции:     (А) вычислить значения функции:   различные   $x$   -   числа подставить в выражение функции и   найти   свои     $y$   -   значения.   (В) составить таблицу: список точек    ($x$; $y$ ),    пары соответствующих   $x$   - чисел и его   $y$   -    значений абсциссы и ординаты. (С) нанести эти   точки   из   списка   на   координатную плоскость   в   соответствии   с   координатами   точек. (Д)   построить график: линию, проходящую   через   все   нанесенные   точки.    Аккуратно, красиво! (Е) при необходимости, дополнить список новыми точками:    подобрать    $x$   -   числа   для   коррекции,   уточнения   графика.

Функция     $y=f\left(x\right)$    - это правило, по которому $x$ - аргументам соответствуют у - значения.    (А) переменная $x$   называется аргументом функции.   (В)   $y$ переменная - значение функции при определенном аргументе.    (С)   $f\left(x\right)$ - Правило, или закон функции - по которому вычисляются значения функции.

Линейная   функция   и   ее   график

Линейной функцией называется функция вида    $y=kx+b$   , где коэффициенты    $k$    и    $b$   -   заданные числа.     Графиком   линейной   функции   является   прямая линия.     Т.к прямая определяется   двумя её точками,   то для   построения   графика функции достаточно   построить   две    точки этого графика.

Пример 1:        Построить график функции   $y=-2x+7$

• правило функции $f\left(x\right)=-2x+7$.        Вычислим несколько значений для различных   $x$ - аргументов:
• $f\left(0\right)=7$      $f\left(1\right)=-2+7=5$        $f\left(2\right)=-4+7=3$         $f\left(6\right)=-12+7=-5$    Таблица значений: $(0;7)$          $(1;5)$         $(2;3)$         $(6;-5)$         $(5;-3)$        $(-3;13)$        $(-1;5)$
• Получили список точек, их координат. Таблица значений. Отметим точки на координатной плоскости. Проведем график.

Пример 2:        Построить график функции   $y=5x+10$

• правило функции $f\left(x\right)=5x+10$.     $f\left(-2\right)=0$      $f\left(-1,5\right)=-7,5+10=2,5$        $f\left(0\right)=10$         $f\left(1\right)=5+10=15$
• Таблица значений: $(-2;0)$             $(-1,5;2,5)$            $(-1;5)$            $(0;10)$            $(1;15)$ . Проведем график.

              

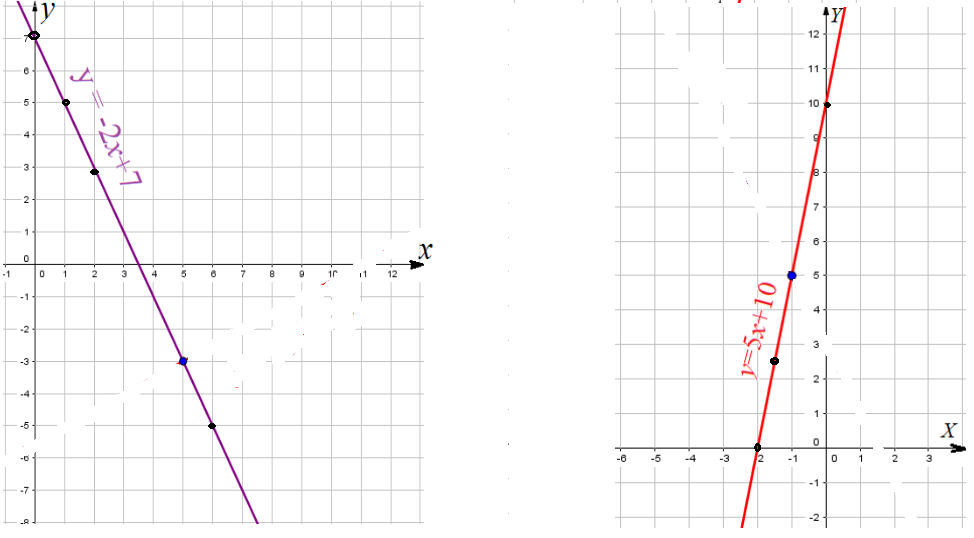
Cвойства   графика   функции        $y=kx + b$

• При    $b=0$   линейная   функция   имеет   вид      $y=kx$.       Прямая   проходит   через начало    координат.
  
• вид      $y=kx$.       Прямая   проходит   через начало    координат: $x=0$ ; $y=0$
• При    $b=0$   линейная   функция   имеет   вид      $y=kx$.       Прямая   проходит   через начало    координат: $x=0$ ; $y=0$
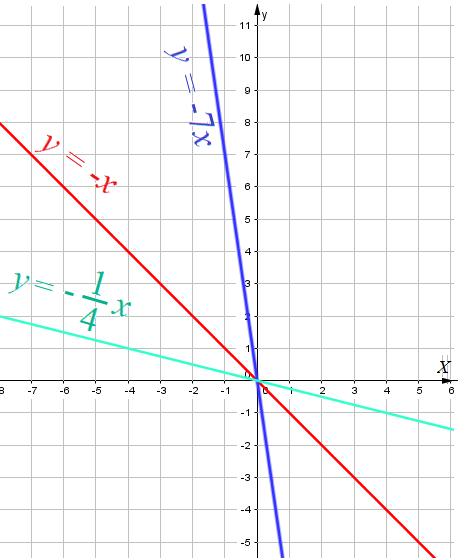
• при        $k > 0$     функция      $y=kx$      возрастает    на   всей   числовой   оси.     (наклон прямой вправо)
• при        $k < 0$   функция      $y=kx$    убывает на   всей   числовой   оси.      (наклон прямой влево)
• График функции    $y=kx+b$   получается сдвигом графика функции     $y=kx$   на     $b$    единиц вдоль оси ординат.
• Графиками функций   $y=kx+b$    и     $y=kx$     являются   параллельные прямые.
• Замечание:     для   построения   графика   удобно   находить   точки   пересечения   с   осями   координат.
• Наклон   графика определяется   $k$ - коэффициентом    функции      $y=kx+a$      при   $x$.   чем   меньше   $k$ - коэффициент, тем   "горизонтальнее".
• Параллельность:    линейные   функции      $y=kx+a$      и      $y=kx+b$      имеют   одинаковые    $k$ - коэффициент   наклона, то   их   графики   -   прямые    параллельны.
• Перпендикулярность:    графики   прямых      $y=kx+a$     и      $y=-\frac{1}{k}x+b$         взаимоперпендикулярны,   произведение коэффициентов   наклона    равен    $-1$.
  

Графическое решение уравнений   

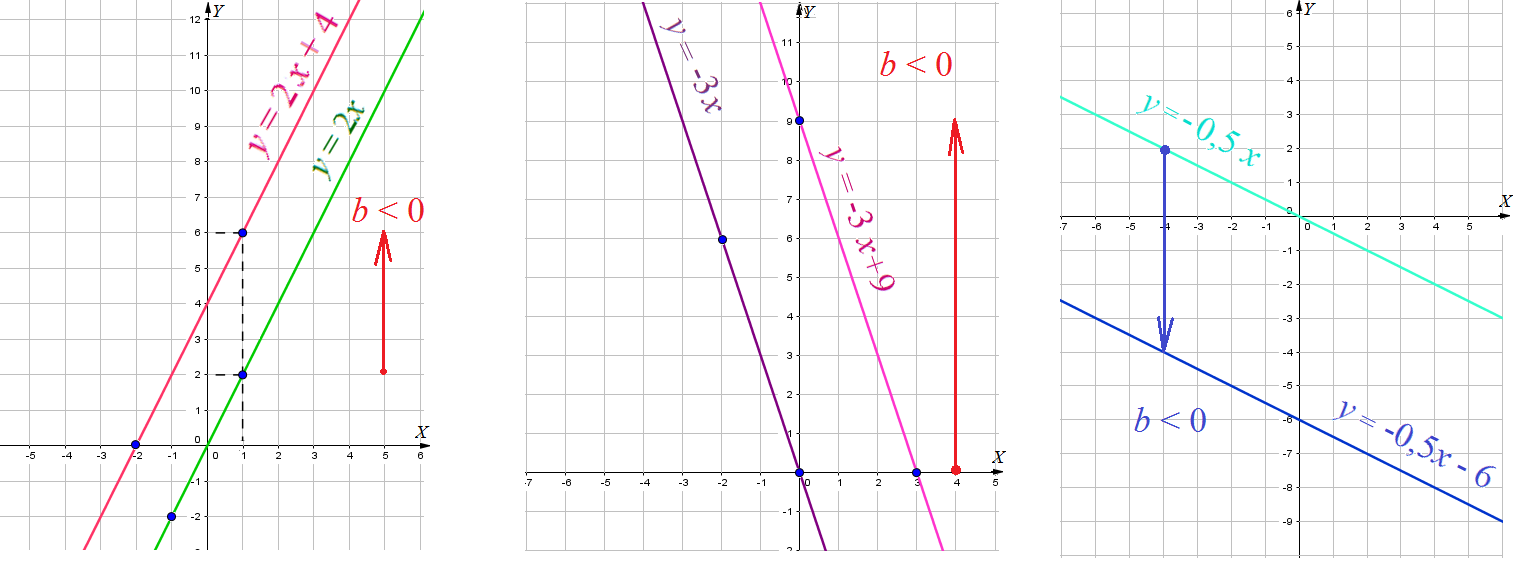
Пример 3:                  Решить уравнение              $-2x+7=0,5x-5,5$                графическим способом.

• Построим   прямые      $y=-2x+7$        и        $y=0,5x-5,5$.     По   чертежу   найдем   точку   пересечения    графиков
  
• $\left(5;-3\right)$.        абсцисса   этой   точки   является   корнем   данного   уравнения,
  
• потому   что,   именно   для   этого    $x$   значения
• графиков,   а   значит   и   функций,   значения   левой   и   правой   частей выравниваются.              ответ:    $x=5$.

            

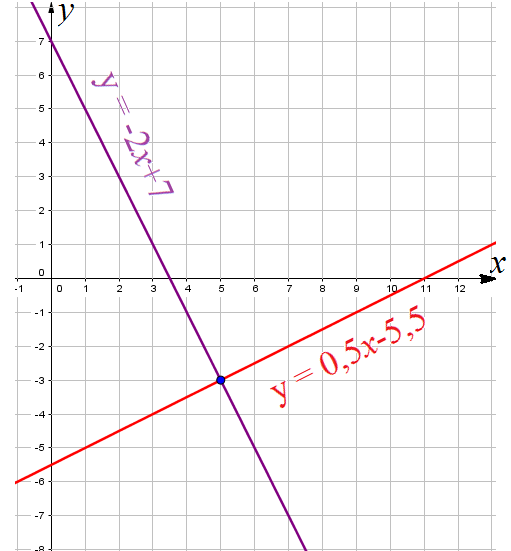
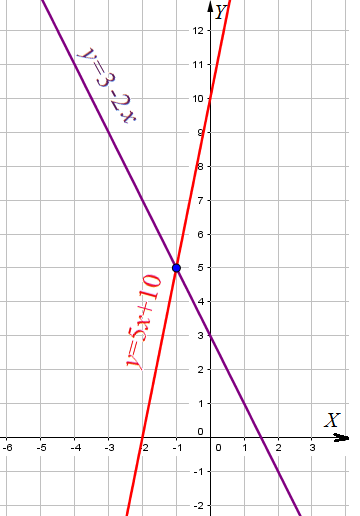
Пример 4:             Решить систему уравнений              {   $2x+y=3$;   $y-5x=10$   }

• Преобразуем   первое   уравнение   системы   к виду     $y=3-2x$,      второе уравнение системы к   виду     $y=5x+10$
• по   чертежу найдем точку пересечения графиков:   $\left(-1;5\right)$.    Координаты   этой точки и являются   решением   системы.
• При таких      $x$    и   $y$    оба    уравнения   системы выравниваются,   значит   такое   решение   удовлетворяет   уравнение.
• ответ:        $x=-1$ ;         $y=5$

Пример 5:                  Найти $b$,    если известно,   что график    $y=\frac{7}{9}x+b$    проходит через точку     $\left(-9;-3\right)$

• Какое число $b=?$, если при аргументе $x=-9$ функция имеет значение $y=-3$ ?   Запишем это в виде условия.
• Координаты заданной точки     $x=-9$ ,     $y=-3$.     Подставим в   уравнение   функции   эти   значения:
• $-3=\frac{7}{9}\left(-9\right)+b$      получим       $-3+7=b$      $\Rightarrow$       $b=4$           ответ:     $b=4$ ,      линейная функция     $y=\frac{7}{9}x+4$.

Линейная   функция   и   ее   график.   Правила.   

Линейное уравнение имеет вид     $ax + by + c = 0$ .     Линейная функция имеет вид      $y=kx+m$        

• Например:         $5x–4y+6=0$ .    Выразим   $y$:     $4y=5x+6$       разделим на    $4$ :      $y=\frac{5x+6}{4}$          $\Rightarrow$       $y=1,25x+1,5$ .
• Полученное уравнение,   равносильно первому,   имеет вид      $y=kx+m$ ,      где:    $k$     и   $m$   —   коэффициенты (параметры).
  
• $x$   —   независимая   переменная - аргумент функции;                 $y$   —   зависимая   переменная - значение функции;         
  

График Дробной функции

Вертикальная асимптота:     $x=5$,   проходит в полюсе, точке разрыва функции.   Точка обнуления знаменателя.   Параллельно $OY$.

Горизонтальная асисмптота:     $y=2$, линия, на которую   "ложится" график при значениях $x$    около   $+-\infty$. Параллельно $OX$.

Гипербола - график простой дроби, две асимптоты делят на 4 четверти, ветви гиперболы "зажаты - прижаты" к асимптотическим линиям .

Пример 6:                Построить график функции     $y=\frac{x-5}{x^2-25}$

• Если выражение функции упрощается, то следует это сделать. Ибо получится функция проще, легче вычисляемая и рисуемая.
• Тождественное преобразование, сокращение      $\frac{x-5}{x^2-25}=\frac{x-5}{(x+5)(x-5)}=\frac{1}{x+5}$. Так, что график $y=\frac{1}{x+5}$ ?
• Не спеши!   Мы сократили на $x-5$ , которое незаконно для $x=5$. Нарушается О.Д.З - в исходной функции нет места $x=5$.
• Значит: можем строить гиперболу $y=\frac{1}{x+5}$ взамен нашей $y=\frac{x-5}{x^2-25}$, но "без точки $x=5$".
• Точка $x=5$ разрывает "гладкий" график гиперболы. Она называется выколотая точка     с координатами $\left(5;0,1\right)$".

Важно уметь исследовать функцию - график около точек разрыва.        + / - поблизости.    Куда тянется?

• Исследуем около   $x=-5$.        Возьмем "близкие" точки $-5,01$ и   $-4,99$.     Вычислим приближенные значения.
• Чуть левее ... $f\left(-5,01\right)=\frac{-5,01-5}{(-5,01)^2-5^2}\approx -100$.         Чуть правее ... $f\left(-4,99\right)=\frac{-4,99-5}{(-4,99)^2-5^2}\approx 100$.
• Прямая   $x=-5$ - вертикальная асимптота. Ветвь слева прижимается "вниз", к     $-\infty$ . А справа поднимается вверх к     $+\infty$.
• Около   $x=5$.    Чуть левее   $f\left(4,99\right)=\frac{4,99-5}{4,99^2-5^2}\approx0,101$.   $f\left(5,01\right)=\frac{5,01-5}{5,01^2-5^2}\approx0,099$.
  
• Значит, $x=5$ точка разрыва, на графике    выколотая точка     $\left(5;0,1\right)$.        Т.к. в ней   $y=\frac{1}{5+5}=0,1$.
• "О нулях":   при   $x=0$    $y=0,2$ .   Но функция нигде не обнуляется, $y\ne0$. Прямая   $y=0$ - горизонтальная асимптота.

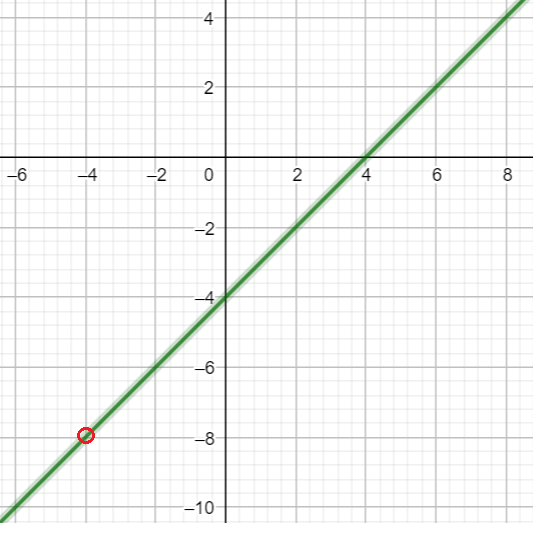
Пример 7:                Построить график функции     $y=\frac{x^2-16}{x+4}$

• О.Д.З   функции    $x\ne-4$. Оговорив это, со спокойной совестью сократим   $y=\frac{x^2-16}{x+4}=x-4$.
• График нащей функции     -     прямая линия       $y=x-4$       с выколотой точкой       $\left(-4;-8\right)$      при   $x=-4$.
• "Близко чуть левее":    $x=-4,01$   значение      $f\left(-4,01\right)=\frac{(-4,01)^2-16}{-4,01+4}=-8,01$.         Ближе?    ...     Предел   $\approx-8$.
• "О нулях".     при   $x=0$    $y=-4$ .    Обнуление функции $y=0$    при    $x=4$ - пересечение с   $x$ - осью.
  

График Дробно - Рациональной Функции.

• Определение:     дробно-рациональной порядка    $\left(n;m\right)$     называется функция вида      $y=\frac{a\cdot x^n+5x^3-x+c}{b\cdot x^m-4x^2-7x+d}$   
• Числитель - многочлен степени   $n$     , знаменатель - многочлен степени    $m$ .       Общий вид:   $y=\frac{P\left(x\right)}{Q\left(x\right)}$
• Нули функции - корни числителя $P\left(x\right)=0$ , Асимптоты (полюсы) - корни знаменателя $Q\left(x\right)=0$.

Система уравнений

Пример 8:      Найти общие точки графиков       $\left(x-3\right)^2+\left(2-y\right)^2=50$     и    $y=3-2x$

• "Общие точки" означает:    пересечение графиков, значит выполнение обеих равенств.
• Значит, надо    решить систему уравнений: найти все такие пары     $(x;y)$ , которые    выравнивают оба равенства системы.
• Стандартный метод: (I). Из какого-либо уравнения    выразить одно неизвестное через другое.   (II).     Подставить во второе уравнение. (III). Решить уравнение от   1 неизвестного.   (IV). Для каждого полученного значения   найти его пару .
• $y=3-2x$ подставим в первое уравнение     $\left(x-3\right)^2+\left(2-\left(3-2x\right)\right)^2=50$   и решим.
• $\left(x-3\right)^2+\left(2x-1\right)^2=50$ $\Rightarrow$   $x^2-6x+9+4x^2-4x+1=50$   $\Rightarrow$    $5x^2-10x-40=0$
• $x^2-6x+9+4x^2-4x+1=50$
• $x^2-2x-8=0$     квадратное уравнение, корни    $x_1=-2$        $x_2=4$
• $x_1=-2$    соответствует значение   $y_1=3-2(-2)=7$.        $x_2=4$ соответствует значение   $y_2=3-2(4)=-1$
  
• Ответ: Точки пересечений графиков     $(-2;7)$    $(4;-1)$.    Меньшая абсцисса    $x=-2$.

IX.       Задания,        Задачи,       Упражнения,     Примеры: