Пример 1: Решить уравнение $\cos x=-\frac{\sqrt{2}}{2}$
- надо найти все значения $x$ , при которых левая часть уравнивается с правой, т.е. углы, чей косинус $-\frac{\sqrt{2}}{2}$,
- т.е. все углы, точки которых на Е.Т.О. имеют $x$ - координатой $-\frac{\sqrt{2}}{2}$. таких бесконечно много,
- а соответствующих точек на Е.Т.О. всего две: одна во $2$-ой четверти $\frac{3\pi}{4}$ со всеми $2\pi$ прокрутками,
- другая $\left(-\frac{3\pi}{4}\right)$ с любым $-+2\pi\cdot n$ . Все эти углы можно записать в виде двух серий решений:
- ответ: $x=\frac{3\pi}{4}+2\pi n$ $x=-\frac{3\pi}{4}+2\pi m$ где $n$ и $m$ целые числа, "полные прокрутки".
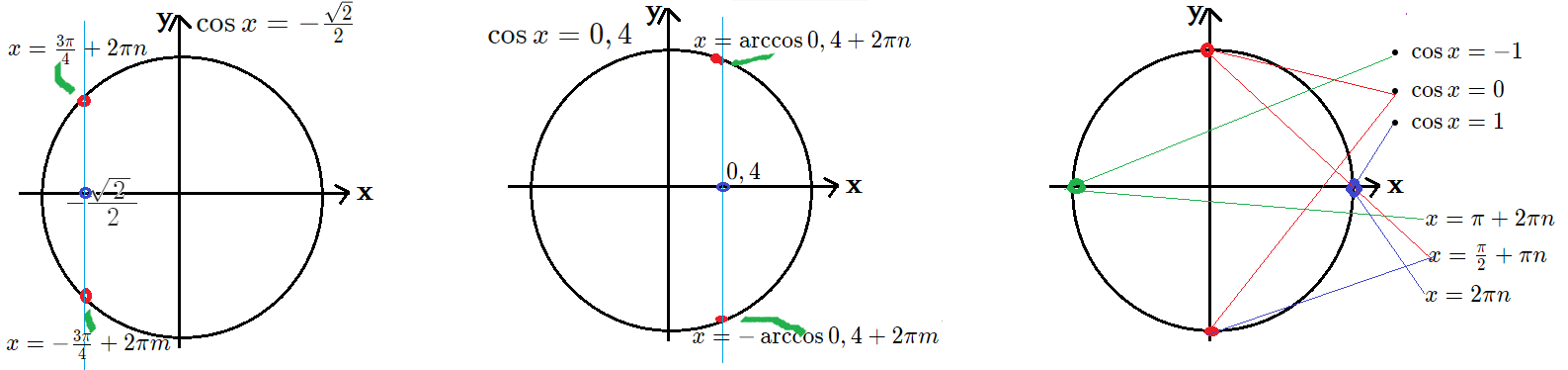
Пример 2: Решить уравнение $\cos x=0,4$
- На Е.Т.О. ровно две точки $x$ - координата которых равна $0,4$. Какие углы изображают эти точки?
- В первой четверти угол $\arccos0,4$ "попадает" в одну из этих точек. В четвертой четверти угол $-\arccos0,4$ имеет нужную $x$ - координату.
- замечание: $\arccos0,4$ есть именно тот угол, чей косинус равен $0,4$. Т.е. его точка имеет $x$ - координату $0,4$.
- Но кроме этих двух углов, в эти точки попадают все углы, "докрученные" на полные обороты. т.е. $-+2\pi\cdot n$, "полные прокрутки".
- ответ: $x=\arccos0,4+2\pi n$ $x=-\arccos0,4+2\pi m$ где $n$ и $m$ целые числа,
Формула решения простейшего косинус - уравнения
- "Простейшим" тригонометрическим уравнением называется cos (что-то от $x$ ) = числу.
- $\cos f\left(t\right)=A$ при $\left|A\right|\le1$ решения: $f\left(t\right)=\arccos A+2\pi n$ и $f\left(t\right)=-\arccos A+2\pi m$ $2$ серии.
- при $\left|A\right| > 1$ решений нет. никакой угол не может иметь координату на Е.Т.О больше единицы.
- Любое уравнение на каком-то этапе процесса решения "приводится" к простейшему виду ... и "вскрывается" по формулам.
Тривиальные случаи: cos равен -1, 0 или 1.
- $\cos x=-1$ $\Rightarrow$ крайняя левая точка на Е.Т.О $\Rightarrow$ $x=\pi+2\pi n$ - одна серия.
- $\cos x= 0$ $\Rightarrow$ две точки на Е.Т.О, верхняя и нижняя $\Rightarrow$ в одну серию $x=\frac{\pi}{2}+\pi n$ пол-оборотов .
- $\cos x= 1$ $\Rightarrow$ одна, правая точка на Е.Т.О $\Rightarrow$ в одну серию $x=2\pi n$

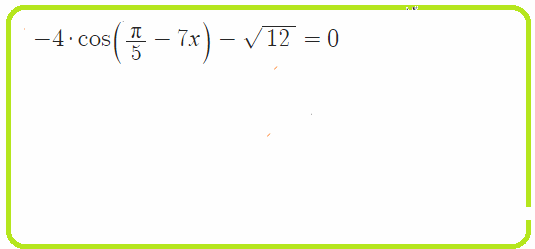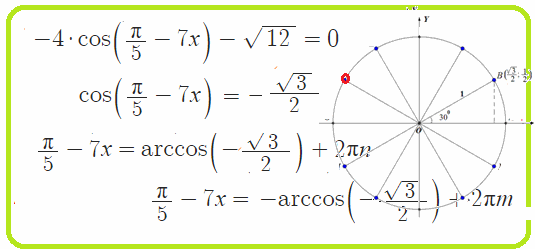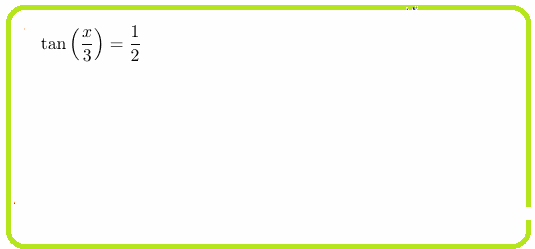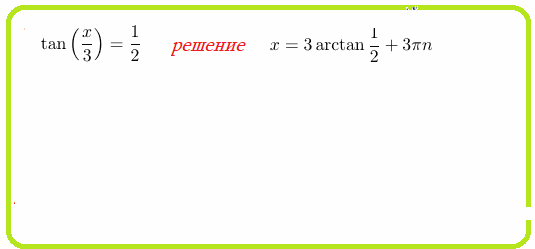
Решения простых тригонометрических уравнений, одна функция, числа
Пример 3: Решить уравнение: $\sqrt{18}+6\cdot\cos\left(\frac{x}{3}\right)=0$
- стратегия: надо выразить функцию, приравнять числа. оголить. получить: функция равна числу, простейшее.
- перенесем слагаемое вправо $6\cdot\cos\left(\frac{x}{3}\right)=-\sqrt{18}$ $\Leftrightarrow$ перенесем туда же множитель $\cos\left(\frac{x}{3}\right)=-\frac{\sqrt{18}}{6}$
- упростим числа справа $\cos\left(\frac{x}{3}\right)=-\frac{3\sqrt{2}}{6}$ $\Leftrightarrow$ еще раз $\cos\left(\frac{x}{3}\right)=-\frac{\sqrt{2}}{2}$ $\Leftrightarrow$ получили: функция = числу.
- первая серия решений : $\frac{x}{3}=-\arccos\left(-\frac{\sqrt{2}}{2}\right)+2\cdot\pi\cdot n$ знак / - / в формуле.
- вторая серия решений : со знаком \ + \ перед арк-косинус $\frac{x}{3}=\arccos\left(-\frac{\sqrt{2}}{2}\right)+2\cdot\pi\cdot m$
- упростим первую $\frac{x}{3}=-\frac{3\pi}{4}+2\cdot\pi\cdot n$ , упростим вторую $\Rightarrow$ $\frac{x}{3}=\frac{3\pi}{4}+2\cdot\pi\cdot m$
- уберем делитель в 1-ой серии $x=3\cdot\left(-\frac{3\pi}{4}+2\cdot\pi\cdot n\right)$ , аналогично во 2-ом $x=3\cdot\left(\frac{3\pi}{4}+2\cdot\pi\cdot m\right)$
- упростим, приукрасим Ответы: $x=-\frac{9\pi}{4}+6\cdot\pi\cdot n$ и $x=\frac{9\pi}{4}+6\cdot\pi\cdot m$ .
Пример 3, еще: Решить уравнение: $18+\sqrt{6}\cdot\cos\left(\frac{x}{3}\right)=0$
- перенесем слагаемое, $\sqrt{6}\cdot\cos\left(\frac{x}{3}\right)=-18$ перенесем множитель $\sqrt{6}$ :
- $\cos\left(\frac{x}{3}\right)=-\frac{18}{\sqrt{6}}$ теперь арккосинус? нет, потому что справа число меньшее $-1$,
- $\arccos\left(-\frac{18}{\sqrt{6}}\right)$ не число, {Цвет:Red инвалид, такое же недорозумение, как например $\sqrt{-9}$.
- Ответ: У уравнения $\cos\left(\frac{x}{3}\right)=-\frac{18}{\sqrt{6}}$ нет решений.
Пример 3: еще Решить уравнение: $\sqrt{6}+18\cdot\cos\left(\frac{t}{3}\right)=0$
- переносы: $18\cdot\cos\left(\frac{t}{3}\right)=-\sqrt{6}$ $\Rightarrow$ $\cos\left(\frac{t}{3}\right)=-\frac{\sqrt{6}}{18}$
- число $-\frac{\sqrt{6}}{18}\approx-\frac{2,5}{18}\approx-\frac{5}{36}\approx-0,2$ находится в интервале $\left[-1;1\right]$, значит, решения есть в виде двух серий
- $\left(\frac{t}{3}\right)=\arccos\left(-\frac{\sqrt{6}}{18}\right) +2\pi n$ $\left(\frac{t}{3}\right)=-\arccos\left(-\frac{\sqrt{6}}{18}\right) +2\pi m$
- арккосинус от минуса следует "переделать" на плюсовой по свойству: $\arccos\left(-a\right)=\pi-\arccos a$
- Тогда, получим $\left(\frac{t}{3}\right)=\pi-\arccos\left(\frac{\sqrt{6}}{18}\right) +2\pi n$ $\left(\frac{t}{3}\right)=-\pi+\arccos\left(\frac{\sqrt{6}}{18}\right) +2\pi m$
- теперь, надо из этих равенств найти $t$. Это легко, если смотреть по проще на эти уравнения: как на простое $\left(\frac{t}{3}\right)=5$.
- Ответы: $t=3\pi-3\arccos\left(\frac{\sqrt{6}}{18}\right) +6\pi n$ $t=-3\pi+3\arccos\left(\frac{\sqrt{6}}{18}\right) +6\pi m$
Напоминание: из свойств арккосинусов
- Арккосинус ( $\arccos a$ ) числа есть единственный угол из интервала $\left[0;\pi\right]$ такой, что $\cos\left(\arccos a\right)=a$
- Если $a>1$ или $a<-1$, то $\arccos a$ не существует, инвалид!
- Для положительных $a$ - чисел $\arccos a$ есть угол из 1-ой четверти, из интервала $\left[0;\frac{\pi}{2}\right]$
- Для отрицательных $a$ - чисел $\arccos a$ - угол из 2-ой четверти, из интервала $\left[\frac{\pi}{2};\pi\right]$
- Формула "передельки" минусового под арккосинусом: $\arccos\left(-\frac{2}{3}\right)=\pi-\arccos\left(\frac{2}{3}\right)$, $\arccos\left(-a\right)=\pi-\arccos\left(a\right)$
- При решении уравнения ответ должен быть записан через арккосинус положительного числа. Нельзя оставлять $\arccos\left(-0,7\right)$
Упражнения A: Решить уравнения
Упражнения В: Решить уравнения
